Influencia de factores climáticos en la regionalización de precipitaciones máximas en la vertiente del Lago Titicaca

Influence of climate factors on the regionalization of maximum precipitations in the basin of Lake Titicaca

Eduardo Flores-Condori^1*; Eduardo Luis Flores-Quispe²; Luis Morales-Aranibar³

1 Universidad Nacional del Altiplano, Puno, Puno. Perú.

2 Universidad Nacional de Moquegua, Ilo, Moquegua. Perú.

3 Universidad Nacional Intercultural de Quillabamba, La Convención, Cusco. Perú.

*Autor corresponsal: eflores@unap.edu.pe (E. Flores-Condori).

ID ORCID de los autores

E. Flores-Condori: https://orcid.org/0000-0003-0983-5250

E. L. Flores-Quispe: https://orcid.org/0000-0001-5106-9583

L. Morales-Aranibar: https://orcid.org/0000-0002-9421-9833

RESUMEN

El objetivo fue determinar la influencia de factores climáticos en la regionalización de las precipitaciones máximas de 24 horas y se incluyó elementos climáticos. Se utilizó precipitación máxima de 24 horas de 29 estaciones meteorológicas, determinándose: precipitación para periodos de retorno, un modelo regional de regresión entre precipitación máxima, factores climáticos y periodo de retorno, parámetros utilizando máxima verosimilitud, zonas homogéneas con análisis clúster, un modelo para cada zona, un modelo lineal y no lineal. Las distribuciones Log Normal tres parámetros y Log Gumbel presentan mejor ajuste a datos. La prueba de Anderson-Darling detectó no normalidad para transformar datos. En el modelo regional de regresión obtuvimos r²=0,388; estadístico Durbin-Watson=0,5456 siendo regresión no espuria. Obtuvimos cinco zonas homogéneas, en la zona 1, 2, 3, 4 y 5 el r² fue 0,932; 0,339; 0,962; 0,863 y 0,99, respectivamente, en las regresiones la mayoría de los factores climáticos son estadísticamente significativos (p < 0,05). El modelo regional lineal y no lineal obtuvieron r² de 0,48 y 0,52, respectivamente. Los modelos no lineales 1, 2 y 3 obtuvieron r²=0,51, 0,51 y 0,50, respectivamente. La influencia de la mayoría de los factores climáticos (altitud, longitud y latitud) en la regionalización de precipitaciones máximas es alta según las regresiones.

Palabras clave: Factores climáticos; regionalización; precipitación máxima; vertiente del lago Titicaca; análisis de clúster.

ABSTRACT

The objective was to determine the influence of climatic factors in the regionalization of the maximum 24-hour rainfall and climatic elements were included. Maximum 24-hour precipitation from 29 meteorological stations was used, determining: precipitation for return periods, a regional regression model between maximum precipitation, climatic factors and return period, parameters using maximum likelihood, homogeneous zones with cluster analysis, a model for each zone, a linear and non-linear model. The three-parameter Log Normal and Log Gumbel distributions present better fit to data. The Anderson-Darling test detected non-normality to transform data. In the regional regression model, we obtained r2 = 0.388; Durbin-Watson statistic = 0.5456 being non-spurious regression. We obtained five homogeneous zones, in zone 1, 2, 3, 4 and 5 the r2 was 0.932; 0.339; 0.962; 0.863 and 0.99, respectively, in the regressions most of the climatic factors are statistically significant (p < 0.05). The linear and non-linear regional model obtained r2 of 0.48 and 0.52, respectively. Nonlinear models 1, 2 and 3 obtained r2 = 0.51, 0.51 and 0.50, respectively. The influence of most of the climatic factors (altitude, longitude and latitude) in the regionalization of maximum rainfall is high according to the regressions.

Keywords: Climatic factors; regionalization; maximum precipitation; slope of Lake Titicaca; cluster analysis.

Recibido: 01-01-2021.

Aceptado: 22-02-2021.

En obras hidráulicas en las que se requiere de un diseño hidrológico, se recurre al uso de curvas intensidad – duración – frecuencia (IDF) para estimar una tormenta asociada a un tiempo de recurrencia y calcular el caudal pico mediante simulación del proceso lluvia-escorrentía. Sin embargo, en muchas zonas de la vertiente del Lago Titicaca existe carencia de datos pluviográficos que permitan confeccionar las relaciones IDF. Por lo que se recurre a la regionalización a fin de cubrir estos vacíos de información, basándose en la hipótesis de la similitud estadística regional.

En la estadística existe varias de funciones de distribución de probabilidad teóricas; De hecho, existen tantas como se quiera, y obviamente no es posible probarlas todas para un problema particular. Por lo tanto, es necesario escoger, de esas funciones, las que se adapten mejor al problema bajo análisis. Entre las funciones de distribución de probabilidad usadas en hidrología, son: Normal, Lognormal, Pearson III y Gumbel. Estas funciones, aun cuando son las más comúnmente usadas en la hidrología aplicada, no son todas, pues el enfoque no es exhaustivo (Aparicio, 2010).

En muchos casos existen curvas estándar de intensidad-duración-frecuencia (IDF) disponibles para un sitio, por lo que no sería necesario este análisis. Sin embargo, es conveniente entender el procedimiento utilizado para desarrollar estas relaciones. Usualmente los datos se presentan en forma gráfica, con la duración en el eje horizontal y la intensidad en el eje vertical, mostrando una serie de curvas, para cada uno de los períodos de retorno de diseño (Chow et al., 1988).

En una investigación de análisis estadístico y regionalización de las precipitaciones utilizando alturas de precipitación anual, diarias e intensidades (Nouvelot et al., 1995), realizaron el siguiente procedimiento. La determinación de la altura pluviométrica promedio anual 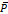, ya sea utilizando una estación de referencia o por interpolación en el mapa de isoyetas. Las estimaciones de las alturas anuales para diversas frecuencias, ya sea a partir de ecuaciones generales derivadas de las leyes estadísticas o mediante las relaciones del tipo (Nouvelot et al., 1995).

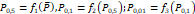
Dónde: P_0,5, P_0,1, P_0,01 = alturas de precipitación anual para una probabilidad de 0,5; 0,1 y 0,01, respectivamente (período de retorno de 2, 10 y 100 años).

La determinación de la precisión de los resultados en función del número de años de observaciones disponible, y las estimaciones de las alturas pluviométricas diarias H para diversos períodos de retorno, a partir de las leyes estadísticas o mediante las relaciones (Nouvelot et al., 1995):

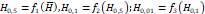
Las estimaciones de diversas frecuencias de las intensidades I (o de las láminas precipitadas h) correspondientes a diferentes intervalos de tiempo t, a partir de las lluvias diarias de igual frecuencia F: I_F = Φ(t,H_F). En muchos proyectos de diseño hidrológico, como el diseño de un drenaje urbano, es la determinación de los eventos de lluvia que deben usarse. La forma más común de hacerlo es utilizar una tormenta de diseño o un evento que involucre una relación entre la intensidad de lluvia, la duración y las frecuencias apropiados para la obra y el sitio (Nouvelot et al., 1995).

Los datos hidrológicos en general, están constituidos por una larga secuencia de observaciones de alguna fase del ciclo hidrológico obtenidas para un determinado lugar. No obstante que un registro largo sea lo deseable, se debe reconocer que cuanto más largo es el período de registro, mayor será la posibilidad de error. Una serie generada en esas condiciones, si los errores o cambios fueran apreciables, es inconsistente, o carece de homogeneidad. Para verificar este tipo de inconsistencia, se usa el método de la curva de doble masa, basado en el hecho de que un gráfico de una cantidad acumulada graficada contra otra cantidad acumulada durante el mismo período, debe ser una línea recta siempre que las cantidades sean proporcionales, la inclinación de la recta representa la constante de proporcionalidad. Una alteración en la pendiente de la recta, indicará que ocurrió un cambio en la constante de proporcionalidad entre las dos variables o que tal vez la proporcionalidad no es constante en todos los niveles de acumulación (Mejía, 2001).

El dimensionamiento de distintos tipos de obras requiere el cálculo de la crecida de diseño para lo cual es necesario asociar una magnitud de crecida con la probabilidad anual de ser superada, con lo que se presenta el riesgo hidrológico del evento (Paoli et al., 2001).

En un trabajo abordaron un método simple de estimación de las precipitaciones máximas en 24 horas, ellos proponen una relación entre la media mensual de precipitación y su valor máximo en 24 horas del tipo potencial (Morales et al., 2005), esto es:

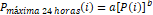
Dónde: P(i) = precipitación media mensual, a y b son constantes a determinar.

Unos investigadores consideraron la frecuencia de precipitaciones medias mensuales como una combinación lineal del lugar de presión máxima en Chile o lpm (Morales et al., 2005 & Saavedra et al., 2002), de tal forma que la ecuación que los relaciona es del tipo:

Dónde: Lat = latitud del lugar considerado y lpm(i) = lugar de presión máxima en Chile para el mes i. Los coeficientes a y b dependen de la latitud (Lat) y longitud (lon) y están dados por:

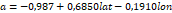
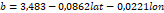
Donde el coeficiente de determinación muestra que las relaciones explican el 87,9% de la variabilidad, además p < 0,01, lo que indica que las variables están relacionadas significativamente con un 99% de confianza. Investigadores calcularon la precipitación máxima en 24 horas a partir de la relación:

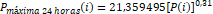
Su modelo explica el 67,2% de la variabilidad, además p < 0,01, indica que los valores de precipitación máxima en 24 horas y los valores medios mensuales están relacionados significativamente con un 99% de confianza (Morales et al., 2005).

Por otra parte, los métodos estadísticos se apoyan en la existencia de series de datos en el lugar de interés, las cuales son sometidas a un análisis de frecuencias usando técnicas tradicionales de estudio. Esto implica que la curva de frecuencia definida para un determinado lugar es válida para ese lugar; la regionalización de datos permite combinar informaciones de diversos lugares en la cuenca, para producir por ejemplo, una curva regional de frecuencias, válida en toda la región y lugares sin información; este recurso entre tanto, está limitado a 100 años de período de retorno (Mochica, 2013).

Los resultados podrían ser confiables siempre que existan suficientes datos disponibles y no hayan ocurrido modificaciones importantes en el régimen de lluvias durante el período de registro, o después; se acepta entonces, la condición de que el comportamiento del sistema continuará siendo el mismo durante el período de cálculo en el futuro (Terrazas, 2013).

La tormenta de diseño estimada a partir de relaciones intensidad – duración – frecuencia, es un parámetro importante en el planeamiento hidrológico de áreas urbanas (Ghazavi et al., 2016).

En la modelación hidrológica la precipitación máxima se utiliza ampliamente, existe el efecto del uso del suelo en la transformación lluvia - escurrimiento. Modelos hidrológicos como SWAT han sido utilizados para evaluar el efecto hidrológico de las transformaciones intensas territoriales como la forestación masiva con especies exóticas (Aguayo et al., 2016). Las curvas intensidad duración frecuencia fueron obtenidas a partir de eventos de precipitación para varios períodos de retorno y duraciones, además para estimar los parámetros de las ecuaciones se utilizó el método de mínimos cuadrados (Ewea et al., 2017). La variabilidad climática asociada al fenómeno de “El niño” tiene una influencia en las precipitaciones disminuyendo estas, así como incrementando las sequias, así mismo el fenómeno de “La niña” tiene un efecto inverso aumentando las precipitaciones y reduciendo las sequias; por consiguiente, es importante incorporar este efecto en el análisis hidrológico (Sedano, 2017).

Dentro del análisis de precipitación en el diseño hidrológico las curvas intensidad – duración – frecuencia son herramientas muy utilizadas. Se construyen a partir de ajuste a distribuciones de probabilidad y estimaciones de parámetros de regresión (John & Brema, 2018).

Una investigación evaluó el efecto del área parcial y su relación con las curvas intensidad - duración – frecuencia, que se utilizan para estimar hidrogramas de diseño con el método racional y también se analizó el problema que se genera cuando la duración de la lluvia crítica es menor al tiempo de concentración (Campos et al., 2020).

En investigaciones anteriores claramente relacionan la frecuencia de precipitación media con factores climáticos como latitud y longitud, a su vez también relacionan la precipitación media con la precipitación máxima (Saavedra et al., 2002 & Morales et al., 2005). Entonces existe una influencia significativa y alta de los factores climáticos sobre la regionalización de precipitaciones en condiciones donde se realizaron estas investigaciones.

Los factores climáticos han sido estudiados en varias investigaciones, tienen mucha importancia porque influyen en los ciclos de vida (Tur et al., 2018), además entre otros factores la topografía principalmente influye en las características del clima en los andes tropicales (Pazmiño, 2019), la topografía tiene relación con la posición geográfica, entonces los factores influyen en las lluvias. Otra investigación hace referencia a factores climáticos de vulnerabilidad y se ha analizado su influencia en la producción agrícola (Abreu et al., 2020). Las precipitaciones en agriculturas de secano influyen mucho en la producción agrícola.

En cuanto a regionalización, otra investigación ha utilizado análisis regional de frecuencias, además también ha determinado seis zonas homogéneas por el método de Hosking y Wallis, recomendando para cada región un función de distribución de probabilidad adecuada (López et al., 2019). En una investigación reciente se realizó modelización matemática de lluvias extremas determinándose relaciones intensidad-duración frecuencia (Suárez-Aguilar et al., 2020).

En esta investigación se determina la influencia de factores climáticos sobre la regionalización de precipitaciones máximas, utilizando modelos empíricos de regresión, se realizó el estudio del efecto de factores climáticos: latitud, longitud y altitud. También en los modelos se incluye elementos climáticos. A fin de establecer modelos regionales para predecir la precipitación máxima en cualquier punto de la vertiente del lago Titicaca, para poder mitigar su efecto socioeconómico.

La vertiente del Lago Titicaca, está delimitada geográficamente entre las coordenadas 14°03' y 20° 00' de Latitud Sur y entre 66° 21' y 71°07' de Longitud Oeste, a una altitud de 3810 m.s.n.m. ubicada en la región de Puno, sus características físico naturales constituye la mayor importancia del sistema hídrico, con una superficie de 8400 km², embalsa un volumen de 932 mil millones de metros cúbicos. Para la modelación, se utilizaron registros meteorológicos del Servicio Nacional de Meteorología e Hidrología Puno, de una longitud de registro no menor de 26 años. Las estaciones meteorológicas utilizadas fueron 29: Ananea, Cojata, Arapa, Ayaviri, Azangaro, Cabanillas, Capachica, Chuquibambilla, Crucero, Huancane, Lampa, Los Uros, Mañazo, Muñani, Pampahuta, Progreso, Pucara, Putina, Capazo, Mazo Cruz, Pizacoma, Desaguadero, Huaraya Moho, Juli, Laraqueri, Puno, Tahuacoyunguyo, Taraco, Isla Taquile.

Los factores climáticos fueron: Latitud, longitud, altitud, y los elementos climáticos fueron: humedad relativa, oscilación de temperatura media, y periodo de retorno de la precipitación máxima.

Se utilizó la prueba de Kolmogorov-Smirnov para seleccionar la distribución que mejor se ajuste a la precipitación máxima. Luego se realizó el análisis de frecuencia de precipitación máxima con la distribución de probabilidad seleccionada, se determinó las precipitaciones máximas para los períodos de retorno de 25, 50, 100 y 200 años. Se determinó un modelo regional utilizando regresión múltiple. Se determinó los coeficientes de asimetría y se evaluó la normalidad de datos con la prueba de bondad de ajuste gráfica y con la prueba de Anderson-Darling. Se ha procedido a la transformación de datos aplicando logaritmos. Los valores transformados han sido utilizados para el modelamiento utilizando regresión. El modelo de regresión múltiple empleado fue: y=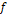(x,θ₁,θ₂,…,θ_n), donde y= precipitación máxima (mm), x = factores climáticos y elementos climáticos, θ_i, i=1,2,…,n = parámetros del modelo. La calibración se realizó aplicando la estimación mínimo cuadrática de coeficientes de regresión lineal múltiple. Sea el modelo de regresión lineal general Y=Xβ+U. Si ese tiene información sobre la función de distribución del error f(u), es posible utilizar el método de la máxima verosimilitud para estimar los parámetros del modelo de manera más eficiente. Si suponemos que los errores son variables aleatorias independientes y normalmente distribuidas, con media cero y varianza constante, se tendría:

U∽NID(0; )

La función de densidad de probabilidad del error, pdf (u_i):

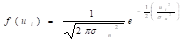
Si los errores, u_i, son variables aleatorias independientes e idénticamente distribuidas (iid), la función de densidad conjunta del vector de errores es:

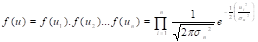
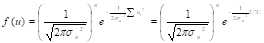
Si reemplazamos U = Y - Xβ en la función conjunta obtendremos la función de verosimilitud,

Con fines de facilitar los cálculos, podemos hallar el logaritmo de la función de verosimilitud o la “log-likelihood function”, l(.) = log (L(.))

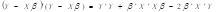
El método de la máxima verosimilitud consiste en maximizar la función de verosimilitud, L(.) o equivalente mente la función de log verosimilitud l(.) con respecto de β y σu², esto es:

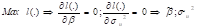
Donde son los estimadores por máxima verosimi-litud de β y , respectivamente, obtenidos de resolver el sistema de ecuaciones simultaneas.

Se determinó un modelo regional de regresión con la precipitación máxima como variable depen-diente y las variables independientes fueron: periodo de retorno, altitud, latitud sur y longitud.

Se aplicó análisis clúster de conglomerados obteniéndose zonas homogéneas. En cada zona homogénea se determinó un modelo de regresión entre la precipitación máxima, periodo de retorno y factores climáticos.

Se determinó un modelo regional lineal de regresión y un modelo regional no lineal de regresión entre precipitación máxima, elementos climáticos (oscilación de temperatura, humedad relativa) y factores climáticos. Además, se determinaron tres modelos no lineales entre precipitación máxima, factores y elementos climáticos.

Las distribuciones Log Normal 3 parámetros y Log Gumbel son las que se ajustan mejor a las precipitaciones máximas de 24 horas en todas las estaciones de la vertiente.

La prueba de normalidad de Anderson Darling obtuvo la probabilidad de excedencia menor a una significancia de 0,05, por tanto, se rechaza la hipótesis nula, hipótesis que afirma que los datos de periodo de retorno son normales. Se ha determinado los coeficientes de asimetría de los datos de las variables, como muestra la tabla 1.

Los valores de coeficiente de asimetría son diferentes de cero, incluso son mayores a 1, se ha procedido a la transformación de datos aplicando logaritmos y los coeficientes de asimetría han bajado considerablemente siendo cercanos a cero, por lo cual se considera haber normalizado los datos.

Tabla 1

Coeficientes de asimetría de las variables

Variable	Símbolo (unidad)	Coeficiente de asimetría
Período de retorno	T (años)	0,67
Precipitación máxima	Pmáx (mm)	1,13
Altitud	Alti (msnm)	1,89
Latitud sur	Lat (grados)	0,60
Longitud oeste	Long (grados)	-0,16

Modelo regional de regresión

Los datos transformados se utilizaron para el modelamiento y los coeficientes de regresión son diferentes de cero al nivel de significancia de 0,05, excepto el coeficiente de la variable transformada latitud que no es significativo estadísticamente. El coeficiente de determinación muestra que solo el 38,8% de la varianza de la precipitación máxima es explicado por las variables independientes y según el análisis de varianza este coeficiente de determinación es diferente de cero siendo significativo, obtuvo también r²_ajustado= 36,5% y desviación típica de S_y = 0,0141. El estadístico Durbin-Watson de 0,5456 es mayor al coeficiente de determinación por lo tanto la regresión no es espuria, además este estadístico al ser mayor a cero muestra que los residuos no están autocorrelacionados.

Dónde: Pmax = precipitación máxima de 24 horas (mm), T = período de retorno (años), Alti = altitud (msnm), Lat = latitud sur (grados), y Long = longitud oeste (grados).

Los residuales siguen una distribución aproximadamente normal según el gráfico de probabilidad normal y el histograma, su variación respecto a los valores ajustados seria casi constante, respecto al orden puede existir un problema de heteroscedasticidad.

Análisis clúster de conglomerados

Se ha observado el bajo ajuste del modelo regional general y se procedió a realizar un análisis clúster para determinar cinco grupos homogéneos de las 29 estaciones meteorológicas en función de los factores del clima: latitud, longitud, altitud y para tiempos de retorno (25, 50, 100 y 200 años). El resultado del análisis clúster definiendo cinco zonas homogéneas, se muestra en la tabla 2.

Tabla 2

Grupos homogéneos de estaciones resultado de análisis clúster

Estaciones	Zona
Ananea, Cojata	I
Arapa, Ayaviri, Azangaro, Cabanillas, Capachica, Chuquibambilla, Crucero, Huancane, Lampa, Los Uros, Mañazo, Muñani, Pampahuta, Progreso, Pucara, Putina	II
Capazo, Mazo Cruz, Pizacoma	III
Desaguadero, Huaraya Moho, Juli, Laraqueri, Puno, Tahuacoyunguyo, Taraco	IV
Isla Taquile	V

Modelo de regresión para la zona I

Según la estimación de parámetros de regresión del modelo para la zona I con una previa transformación de datos a normales, muestra que los coeficientes de regresión del período de retorno son diferentes de cero al nivel de significancia de 0,05, pero el coeficiente de la variable transformada altitud no es significativo estadísticamente. El coeficiente de determinación muestra que 93,2% de la varianza de la precipitación máxima es explicado por las variables independientes y según el análisis de varianza este coeficiente de determinación es significativamente diferente de cero al 0,05. El estadístico Durbin-Watson es mayor al coeficiente de determinación por lo tanto la regresión no es espuria, además este estadístico al ser mayor a cero muestra que los residuos no están autocorrelacionados, el modelo generado para la zona I, es:

Dónde las variables se han descrito anteriormente. Las variables latitud y longitud no fueron consideradas en el modelo por que generan multicolinealidad con las demás variables independientes y además en este grupo sólo se tiene dos estaciones.

Modelo de regresión para la zona II

Se realizó la estimación de parámetros de regresión del modelo para la zona II con una previa transformación de datos a normales. Se hizo también la prueba gráfica de normalidad, el coeficiente de la variable transformada período de retorno es el único que es estadísticamente diferente de cero al nivel de significancia 0,05, en cambio los coeficientes de las otras variables independientes no lo son. El 33,9% de la varianza de la precipitación máxima está explicado por las variables independientes, siendo este coeficiente de determinación estadísticamente diferente de cero según el análisis de varianza al 95% de confianza. Como el coeficiente de determinación es menor al estadístico de Durbin-Watson, entonces la regresión no es espuria, además este estadístico de Durbin-Watson al ser mayor a cero muestra que los residuos no están autocorrelacionados. La forma del modelo para la zona II es:

Dónde las variables se han descrito anteriormente.

Modelo de regresión para la zona III

Se estimó los parámetros de regresión del modelo para la zona III, con una previa transformación de datos a normales, se hizo la prueba gráfica de normalidad, los resultados muestran que los coeficientes son significativos al nivel de confianza de 95%. La varianza de la precipitación máxima transformada es explicada en un 96,2% por las variables independientes transformadas. El coeficiente de determinación es diferente de cero al nivel de significancia de 0,05. El estadístico de Durbin-Watson es mayor a cero por lo tanto no existe auto-correlación entre los residuos. Además, este estadístico a no ser muy menor al coeficiente de determinación está mostrando que la regresión no es espuria. El modelo obtenido se expresa:

Pmax =

(1,5281-0,020893log₁₀T+0,00004689Alt-0,089414Lat)^-1/0,4538

Dónde las variables se han descrito anteriormente. La longitud no se consideró debido a que genera un problema de multicolinealidad con otras variables independientes.

Modelo de regresión para la zona IV

Los parámetros de regresión del modelo para la zona IV también se obtuvieron, con una previa transformación de datos a normales. Se realizó las transformaciones, se hizo la prueba gráfica de normalidad, los coeficientes son significativos para todas las variables independientes excepto para la variable latitud, al nivel de confianza de 95%. La varianza de la precipitación máxima transformada es explicada en un 86,3% por las variables independientes transformadas. El coeficiente de determinación es diferente de cero al nivel de significancia de 0,05. El estadístico de Durbin-Watson es mayor a cero por lo tanto no existe auto-correlación entre los residuos y como es mayor al coeficiente de determinación se considera que la regresión no es espuria.

Dónde las variables se han descrito anteriormente.

Modelo de regresión para la zona V

La estimación de parámetros de regresión del modelo para la región V también fue realizada, la transformación previa a datos a normales no fue necesaria puesto que se utilizó un modelo no lineal potencial. En este grupo solo existe una estación la cual es la Isla Taquile por lo cual los factores climáticos no se pueden utilizar como predictores. A continuación, se presenta la ecuación de regresión potencial para la Isla Taquile, que obtuvo un r² = 0,99:

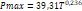
Donde las variables se han descrito anteriormente.

Influencia de factores y elementos climáticos en la precipitación máxima

Se ha optado en relacionar la precipitación máxima con factores climáticos y la intervención de los elementos climáticos: oscilación de temperatura media anual y el porcentaje de humedad juntamente con los factores climáticos. La prueba t de coeficiente de regresión indica que las variables que presentan coeficientes significativos son el periodo de retorno, la oscilación de temperatura y la humedad relativa al 95% de confianza, las demás variables no presentan coeficientes significativa-mente diferentes de cero. El 48% de la variación de la precipitación máxima es explicado por las variables independientes. La regresión no es espuria puesto que r² < Durbin-Watson. La ecuación obtenida es:

Dónde: Osc = oscilación media de temperatura (°C), HR = humedad relativa media (%) y las demás variables se han descrito anteriormente.

La prueba t indica que los logaritmos de las variables que presentan coeficientes significativos son el periodo de retorno y la oscilación de temperatura al 95% de confianza, los demás logaritmos de las variables no presentan coeficientes significativamente diferentes de cero. El 52% de la variación de la precipitación máxima es explicado por las variables independientes. La regresión no es espuria puesto que R² < Durbin-Watson. La ecuación obtenida es la siguiente.

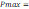
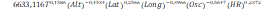
Donde las variables se han descrito anteriormente.

Modelo de Regresión no lineal 1 entre factores, elementos climáticos y precipitación máxima

En este modelo solo se tomó en cuenta las variables independientes el periodo de retorno, la altitud, la oscilación media de la temperatura y la humedad relativa, omitiéndose la latitud sur y la longitud oeste.

La prueba t indica que los logaritmos de las variables que presentan coeficientes significativos son el periodo de retorno y la oscilación de temperatura al 95% de confianza, los demás logaritmos de las variables no presentan coeficientes significativamente diferentes de cero. El 51% de la variación de la precipitación máxima es explicado por las variables independientes. La regresión no es espuria puesto que R2 < Durbin-Watson. La ecuación obtenida es la siguiente.

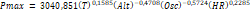
Dónde las variables se han descrito anteriormente.

Modelo de Regresión no lineal 2 entre elemen-tos climáticos y precipitación máxima

En este modelo solo se tomó en cuenta las variables independientes el periodo de retorno, la oscilación media de la temperatura y la humedad relativa, omitiéndose la altitud, la latitud sur y la longitud oeste.

La prueba t indica que los logaritmos de las variables que presentan coeficientes significativos son el periodo de retorno y la oscilación de temperatura al 95% de confianza, los logaritmos de la variable humedad relativa media no presenta un coeficiente significativamente diferente de cero. El 51% de la variación de la precipitación máxima es explicado por las variables independientes. La regresión no es espuria puesto que R² < Durbin-Watson. La ecuación obtenida es la siguiente:

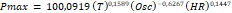
Dónde las variables se han descrito anteriormente.

Modelo de Regresión no lineal 3 entre elementos climáticos y precipitación máxima

En este modelo solo se tomó en cuenta las variables independientes el periodo de retorno y la oscilación media de la temperatura, omitiéndose la humedad relativa, la altitud, la latitud sur y la longitud oeste. La prueba t indica que los logaritmos de las variables que presentan coeficientes significativos diferentes de cero, son el periodo de retorno y la oscilación de temperatura al 95% de confianza. El 50% de la variación de la precipitación máxima es explicado por las variables independientes. La regresión no es espuria puesto que R² < Durbin-Watson = 0,52. La ecuación obtenida es la siguiente.

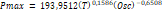
Dónde: Pmax = precipitación máxima en 24 horas (mm), T = periodo de retorno (años), Osc = oscilación media de temperatura (°C).

En la presente investigación se han usado distribu-ciones de probabilidad, como lo han hecho otras investigaciones para obtener precipitaciones máximas para varios períodos de retorno similar al procedimiento para curvas intensidad – duración frecuencia (Ghazavi et al., 2016), también otras investigaciones han utilizado la distribución Gumbel para estimar precipitaciones máximas (Ewea et al., 2017). Así mismo para el análisis de frecuencia se ha utilizado la distribución de Gumbel (John & Brema, 2018) pero con los logaritmos de los datos. Una precipitación máxima siempre está asociada a un periodo de retorno. A comparación en otro estudio se realizó una relación empírica entre la precipitación máxima de 24 horas y la precipitación mensual (Morales et al., 2005).

El modelo regional propuesto tiene como hipótesis que la precipitación máxima es explicada por factores climáticos y la frecuencia (periodo de retorno). Los factores climáticos considerados fueron: latitud, longitud y altitud, lo mismo que otros autores (Morales et al., 2005; Saavedra et al., 2002), que relacionan la frecuencia de precipitación máxima de un mes (i) con el lugar de presión máxima del mes (i), con la latitud y la longitud, entonces el modelo planteado en la presente investigación tiene base en la literatura revisada. Varios autores utilizaron modelos no lineales que predicen la precipitación máxima del mismo modo que los resultados de la presente investigación, por ejemplo, utilizaron modelos potenciales y lineales combinados (Morales et al., 2005; Saavedra et al., 2002).

En investigaciones el elemento climático que utilizaron como predictor de la precipitación máxima fue la precipitación media en un modelo potencial (Morales et al., 2005), en cambio en la presente investigación se propone predecir la precipitación máxima a partir de factores climáticos, periodo de retorno y elementos climáticos (oscilación media de la temperatura y de la humedad relativa media). La influencia sobre la regionalización de la precipitación máxima, de la oscilación media de temperatura es inversa y de la humedad relativa media es directa, así mismo, la influencia del periodo de retorno es directa, en las investigaciones anteriores (Saavedra et al., 2002) no se utilizaron estas variables explicativas.

En estos modelos la variable que posee mayor influencia en la regionalización de la precipitación máxima es el periodo de retorno seguido por factores climáticos como altitud y la latitud dependiendo de la zona. Estos resultados muestran consistencia con la influencia de la latitud y longitud en la frecuencia de precipitación mostrada por otros estudios (Morales et al., 2005; Saavedra et al., 2002).

En el estudio revisado (Morales et al., 2005) no se tuvo en cuenta los elementos climáticos considerados en la presente investigación. Se han obtenido resultados consistentes con investigaciones anteriores que relacionan la precipitación o características de esta con factores climáticos como la latitud y longitud (Saavedra et al., 2002; Morales et al., 2005).

Los factores climáticos tienen mucha importancia porque influyen en los ciclos de vida (Tur et al., 2018), los ciclos de vida depende mucho de la precipitación, la presente investigación muestra que los factores influyen en el régimen de lluvias, además la topografía principalmente influye en las características del clima en los andes tropicales (Pazmiño, 2019), la topografía tiene relación con la posición geográfica, lo cual ha sido evidenciado al encontrar variables significativas como latitud, longitud y altitud para condiciones de la vertiente del Lago Titicaca.

En la presente investigación se ha obtenido cinco regiones homogéneas, también como otra investigación (López et al., 2019) que ha obtenido seis regiones homogéneas, pero con un método diferente, utilizando además análisis regional de frecuencias, además también en cada región se ha obtenido distribuciones de probabilidad adecuadas.

Los factores climáticos generan vulnerabilidad y tienen influencia en la producción agrícola (Abreu et al., 2020). La precipitación en agricultura de secano influye mucho en la producción agrícola. En la presente investigación se ha tratado con precipitación máxima que además de satisfacer las necesidades de cultivos puede generar desastres, al conocer la influencia de los factores climáticos en la regionalización de lluvias extremas, puede predecirse y disminuir sus efectos adversos.

La presente investigación al igual que una reciente, realizó modelización matemática de lluvias extremas (Suárez-Aguilar et al., 2020), a través de los modelos y de la significancia de las variables predictoras se puede conocer el grado de influencia de los factores climáticos sobre la regionalización de lluvia máxima. Por lo tanto, existe una influencia significativa y alta de los factores climáticos sobre la regionalización de la precipitación máxima.

Abreu, M. A., Tenezaca, D. B. O., & Yaguar Mariño, J. J. (2020). Determinacion del grado de influencia de los factores climáticos de vulnerabilidad del sector agropecuario con tecnicas neutrosóficas. Investigacion Operacional, 41(5), 699–705.

Aguayo, M., Stehr, A., & Link, O. (2016). Respuesta hidrológica de una cuenca de meso escala frente a futuros escenarios de expansión forestal. Revista de Geografia Norte Grande, 65, 197–214.

Aparicio, F. J. (2010). Fundamentos de hidrología de superficie. Limusa. https://books.google.com.pe/books?id=6vIKxQEACAAJ

Campos, J. N. B., de Carvalho Studart, T. M., Filho, F. de A. de S., & Porto, V. C. (2020). On the rainfall intensity–duration–frequency curves, partial-area effect and the rational method: Theory and the engineering practice. Water (Switzerland), 12(10).

Chow, V. Te, Maidment, D. R., & Mays, L. W. (1988). Applied hydrology (letters). In Applied Hydrology.

Ewea, H. A., Elfeki, A. M., & Al-Amri, N. S. (2017). Development of intensity–duration–frequency curves for the Kingdom of Saudi Arabia. Geomatics, Natural Hazards and Risk, 8(2), 570–584.

Ghazavi, R., Moafi Rabori, A., & Ahadnejad Reveshty, M. (2016). Modelling and assessment of urban flood hazards based on rainfall intensity-duration-frequency curves reformation. Natural Hazards and Earth System Sciences Discussions, October, 1–19.

John, A. S., & Brema, J. (2018). Analysis of rainfall by intensity-duration- frequency (idf) curves for vamanapuram river basin, kerala. International Journal of Civil Engineering and Technology, 9(7), 403–411.

López, J. J., Goñi, M., San Martín, I., & Erro, J. (2019). Análisis regional de frecuencias de las precipitaciones diarias extremas en Navarra. Elaboración de los mapas de cuantiles. Ingeniería Del Agua, 23(1), 33.

Mejía, J. (2001). Hidrologia Aplicada. DRAT, FIA-UNALM.

Mochica, E. (2013). Análisis de máximas avenidas con fines de diseño de defensa del rio Chichanaco de la ciudad de Sandia. Universidad Nacional del Altiplano.

Morales, L., Casanova, M., Castellaro, G., & Mattar, C. (2005). Método simple para la estimación de la precipitación máxima en 24 horas en la zona central de Chile. X Congreso de Ciencias Del Suelo.

Nouvelot, J.-F., Le Goulven, P., Aleman, M., & Pourrut, P. (1995). Análisis estadístico y regionalización de las precipitaciones en el Ecuador. El Agua En El Ecuador : Clima, Precipitaciones, Escorrentia, 27–66.

Paoli, C., Cacik, P., & Morresi, M. (2001). Consistencia en la determinación de crecidas de diseño por transformación lluvia-caudal y análisis de frecuencia (estudio de un caso). Ingenieria Hidraulica En Mexico, 16(1), 87–97.

Pazmiño, D. (2019). Peligro de incendios forestales asociado a factores climáticos en Ecuador Forest fire hazard associated with climatic factors in Ecuador.

Saavedra, N., Müller, E. P., & Foppiano, A. J. (2002). Monthly mean rainfall frequency model for the central Chilean coasts: Some climatic inferences. International Journal of Climatology, 22(12), 1495–1509.

Sedano, R. K. (2017). Influencia de la variabilidad climática y factores antrópicos en los extremos hidrológicos en el Valle Alto del río Cauca, Colombia. In Doctoral Thesis.

Suárez-Aguilar, Z. E., Sepúlveda-Delgado, O., Patarroyo-Mesa, M., & Canaria-Camargo, L. C. (2020). Modelo matemático para estimar curvas de intensidad, duración y frecuencia de lluvias extremas en Tunja, Colombia. Información Tecnológica, 31(1), 193–206.

Terrazas, J. E. G. (2013). “Análisis comparativo de metodologías para la determinación de descargas máximas para la sub cuenca del rio Ayaviri.” Universidad Nacional del Altiplano.

Tur, B. R., Ricardo, L. A. F., & Velázquez, A. F. (2018). Actividad diaria de Polymita muscarum ( Gastropoda : Cepolidae ) en un agroecosistema : relación con factores climáticos y duración del apareamiento relationship with climatic factors and mating duration. 6, 1–9.