Comparación
de tres coeficientes de similitud para análisis con marcadores moleculares AFLP
en Lupinus mutabilis Sweet
Comparison
of three coefficients of similarity for analysis with molecular markers AFLP in
Lupinus mutabilis Sweet
Roberto F. Aubert-Carreño1,
*; Mercedes Maritza Quispe-Flórez2; Griselda Muñiz-Durán2;
Raúl Humberto Blas-Sevillano3
1 Estación
Experimental Agraria Andenes, Dirección de Desarrollo Tecnológico, Instituto
Nacional de Innovación Agraria, Estación Experimental Agraria Andenes. Av. Micaela
Bastidas N°314-316, Wanchaq, Cusco 08002, Perú.
2 Facultad de
Ciencias. Escuela Profesional de Biología, Universidad Nacional de San Antonio
Abad del Cusco. Av. de la Cultura, Nro. 733, Cusco, Cusco 08001, Perú.
3 Facultad de
Agronomía, Universidad Nacional Agraria La Molina. Av. La Molina s/n - La
Molina, Lima 15012, Perú.
*Autor
corresponsal: rober_auber@hotmail.com (R. F.
Aubert-Carreño)
ID
ORCID de los autores
R.F.
Aubert-Carreño:  https://orcid.org/0000-0002-3350-0947 M.M.
Quispe-Flores:
https://orcid.org/0000-0002-3350-0947 M.M.
Quispe-Flores:  https://orcid.org/0000-0003-2682-6188
https://orcid.org/0000-0003-2682-6188
J.G.
Muñiz-Durán:  https://orcid.org/0000-0001-9988-4827
https://orcid.org/0000-0001-9988-4827
RESUMEN
Se utilizaron tres
coeficientes de similitud: Simple Matching (SM), Jaccard (J) y Dice (D) para
analizar la variabilidad genética mediante el uso de marcadores moleculares
AFLP en 48 accesiones de Lupinus mutabilis Sweet, 26 provenientes del
Departamento de Cusco y 22 de departamentos y países distintos (Ecuador y
Bolivia). A partir de matrices de similitud, se generaron dendrogramas con cada
coeficiente, mediante el método UPGMA a través del software NTSYSpc versión
2.01, analizándose y comparándose entre sí, obteniendo un Coeficiente de
correlación cofenética (r): SM=0,68674, J=0,79116 y D=0,79332; un Índice de
consenso (Clc): SM–J=0,52, SM–D=0,52 y J–D=0,93; y niveles de similitud:
SM=0,68, J=0,39 y D=0,56. Determinándose el coeficiente de Simple Matching como
el más idóneo para análisis de variabilidad genética con marcadores dominantes
como AFLP en L. mutabilis Sweet.
Palabras
clave:
Simple
Matching; Jaccard; Dice; Lupinus mutabilis; AFLP.
ABSTRACT
Three similarity
coefficients were used: Simple Matching (SM), Jaccard (J) and Dice (D) to
analyze genetic variability through the use of AFLP molecular markers in 48 Lupinus
mutabilis Sweet accessions, 26 from the Department of Cusco and 22 from
different departments and countries (Ecuador and Bolivia). From similarity
matrices, dendrograms were generated with each coefficient, using the UPGMA
method through the NTSYSpc software version 2.01, analyzing and comparing each
other, obtaining a coefficient of co-phenetic correlation (r): SM = 0.68674, J
= 0.79116 and D = 0.79332; a Consensus Index (Clc): SM – J = 0.52, SM – D = 0.52
and J – D = 0.93; and levels of similarity: SM = 0.68, J = 0.39 and D = 0.56.
The Simple Matching coefficient was determined as the most suitable for
analysis of genetic variability with dominant markers such as AFLP in L.
mutabilis Sweet.
Keywords: Simple
Matching; Jaccard; Dice; Lupinus mutabilis; AFLP.
Recibido: 10-04-2021.
Aceptado: 05-09-2021.
El género Lupinus incluye
casi 300 especies, pero solo cuatro juegan un papel importante en la
agricultura: L. albus, L. angustifolius, L. luteus y L. mutabilis
(Gresta et al., 2017) (Gulisano et al., 2019). La
especie L. mutabilis Sweet (tarwi), de contenido elevado de proteínas y
aceites (Atchison, 2016), llega a contener un 51% de proteína (Quiñones, 2019)
y por encima del 20% de ácidos grasos en semillas (Galek, 2017). Este posee la
mayor calidad de grano de todos los altramuces cultivados y está adaptada a la
agricultura de bajos insumos en climas templados. La combinación de estas
características convierte a L. mutabilis en una alternativa
potencialmente superior a las fuentes actuales de proteínas y aceites vegetales
(Gulisano et al., 2019); así también, el Tarwi exhibe rasgos clave de
domesticación, que incluyen vainas indehiscentes y semillas con tegumento
permeable, que representan un cultivo de importancia local en varias áreas
andinas (Guilengue et al., 2020). No obstante, diversos factores sociales desprestigia-ron
su consumo, limitando su estudio (Martínez et al., 2015; Martínez, 2015),
siendo pertinente desarrollar investigación de la variabilidad genética de esta
especie, puesto que existe pocos estudios usando marcadores moleculares
(Chirinos-Arias, 2015), en tanto, como mencionan Guillengue et al. (2020), el
establecimiento de programas de mejoramiento y conservación, e incluso la
introducción de este cultivo, depende en gran parte, del profundo conocimiento
de la variabilidad genética intraespecífica de las colecciones.
Uno de los enfoques que se
usa en estudios de diversidad genética se basa en comparaciones de genotipos
individuales dentro y entre las poblaciones (Kosman & Leonard, 2005). El
primer paso en este proceso consiste en elegir las unidades u objetos a
clasificar, es decir las OTU (Operational Taxonomy Unit) (Sokal & Sneath,
1963). Según Crisci & López (1983), los procesos clasificatorios se basan
en las diferencias de los objetos (caracteres) y los valores que ese carácter
puede presentar, se les considera estados. En el presente estudio se utilizaron
marcadores moleculares AFLP (Amplified Fragment Lenght Polymorphisms),
marcadores dominantes (Vos et al., 1995) ventajosos para el estudio de cada
sujeto y de la población (Suárez-Contreras, 2018), con los que se obtiene un
perfil molecular característico independiente de las condiciones ambientales y
del crecimiento de la planta (Remón-Gamboa & Peña-Rojas, 2018), los datos
generados son de tipo doble estado: presencia-ausencia (Moscoe & Emshwiller,
2015), pudiendo generar muchos marcadores de ADN aleatorios en una sola
amplificación por PCR.
Reif et al. (2005) sugieren
el término "alelo informativo" si las frecuencias alélicas se pueden
determinar a partir de los datos de marcadores moleculares, y el término
"alelo no informativo" si no pueden hacerlo. Entonces, cuando los
datos generados por los marcadores moleculares son "alelos no
informativos", como es el caso de los marcadores dominantes, las
estimaciones de los coeficientes entre OTU basándose en la ausencia o presencia
de bandas observadas, se pueden calcular por uno de los tres coeficientes de similaridad:
1)
Simple
matching: SSM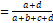
2)
Jaccard:
SJ
3)
Dice:
SD
Se denota: 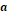 = número de posiciones con
bandas compartidas para los individuos (1-1);
= número de posiciones con
bandas compartidas para los individuos (1-1); 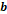 = número de posiciones en
las que el individuo i1 tiene una banda, pero i2
no lo hace (1-0);
= número de posiciones en
las que el individuo i1 tiene una banda, pero i2
no lo hace (1-0);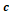 = número de posiciones en
las que el individuo i2 tiene una banda, pero i1
no lo hace (0-1); y
= número de posiciones en
las que el individuo i2 tiene una banda, pero i1
no lo hace (0-1); y 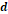 = número de posiciones con
bandas ausentes compartidas para los individuos (0-0) (Sokal & Sneath,
1973), siendo el coeficiente SSM el único de los tres que considera bandas
ausentes compartidas. El coeficiente de Jaccard creado para análisis en
fitología (Jaccard, 1912) funciona bien con datos binarios y así como el
coeficiente Dice mide la similitud directamente, esto lo hace fácil de
implementar y rápido en el cálculo (Bero et al., 2017). Muchas investigaciones
utilizan el coeficiente de Jaccard para medir similitudes en varios campos
(Duarte et al., 1999; Loh et al., 2016).
= número de posiciones con
bandas ausentes compartidas para los individuos (0-0) (Sokal & Sneath,
1973), siendo el coeficiente SSM el único de los tres que considera bandas
ausentes compartidas. El coeficiente de Jaccard creado para análisis en
fitología (Jaccard, 1912) funciona bien con datos binarios y así como el
coeficiente Dice mide la similitud directamente, esto lo hace fácil de
implementar y rápido en el cálculo (Bero et al., 2017). Muchas investigaciones
utilizan el coeficiente de Jaccard para medir similitudes en varios campos
(Duarte et al., 1999; Loh et al., 2016).
Según Duarte et
al. (1999) los resultados de la agrupación pueden estar influenciados por la
elección del coeficiente de similitud y muchas veces los autores no justifican
la elección del o los coefi-cientes utilizados, razón que evidencia la
necesidad de que los mismos deben ser más estudiados, de modo que sea empleado
el más eficiente depen-diendo de la situación. En el presente trabajo se
comparan los coeficientes de similaridad buscando determinar el más idóneo
acorde a la especie en estudio y a los marcadores moleculares utilizados.
Material
vegetal. En el laboratorio de Biología Molecular de
la Escuela Profesional de Biología, Facultad de Ciencias de la Universidad
Nacional de San Antonio Abad del Cusco (UNSAAC), cuyas coordenadas geográficas
son 13°31′18″ latitud sur y 71°57′31″ longitud oeste,
con temperatura controlada que osciló entre 8 °C y 18 °C; con humedad relativa
entre 52% y 60%; se sembraron semillas de 48 accesiones de L. mutabilis
Sweet proporcionadas por el Banco de Germoplasma de la Granja K’ayra de la
UNSAAC, a partir de las que se extrajo el ADN a ser analizado.
Marcadores
AFLP. En el Área de
Biología Molecular del Instituto de Biotecnología (IBT) de la Universidad
Nacional Agraria La Molina se desarrolló el análisis con marcadores AFLP
siguiendo el protocolo de Vos et al. (1995). Amplificados los fragmentos
de ADN, fueron separados vía electroforesis en geles de poliacrilamida y luego
teñidos con Nitrato de Plata. La lectura y enumeración de bandas tomó en cuenta
aquellas con mejor resolución.
Análisis
de similitud genética: Los
datos binarios del conteo de los fragmentos amplificados se registraron en una
hoja de cálculo Microsoft Excel 2015. Cada banda o fragmento de ADN, generado
por cada combinación de iniciadores, se consideró como un locus individual con
dos posibles alelos: presencia de banda, se le asignó el número 1; ausencia de
banda, se le asignó el valor 0. A las bandas de presencia dudosa se les asigno
el número 9. La similitud genética se calculó utilizando los coeficientes de
similitud Simple Matching (SM), Jaccard (J) y Dice (D), obteniéndose tres
matrices de similitud. Se utilizó el software NTSYSpc versión 2.01 (Applie
Biostatistics Inc., Setauket, Nueva York, EE.UU.).
La
comparación de los coeficientes de similitud se realizó a partir del análisis
de las representaciones gráficas (dendrogramas), de la medición de la
distorsión y del índice de consenso:
Representación
gráfica: Obtenida la
matriz de similitud, mediante la técnica de ligamiento “media aritmética no
ponderada” (UPGMA, “unweihted pair-group method using arithmetic averages”) se
elaboró el dendrograma donde las OTU son incorporadas a núcleos o grupos ya
formados tomando en cuenta que el valor de la similitud entre las OTU
candidatas a incorporarse y el núcleo o grupo es igual a una similitud promedio
resultante de los valores de similitud entre la candidata y cada uno de los
integrantes del núcleo o grupo. Si la candidata a incorporarse es un núcleo o
grupo, el valor de similitud será el promedio de los valores de similitud entre
los pares posibles de OTU provenientes de cada núcleo o grupo (González-Andrés &
Pita, 2001); dentro del módulo SAHN del programa NTSYS-pc versión 2.01.
Medición
de la distorsión: Se
utilizó el coeficiente de correlación cofenética (r), establecido por
Sokal & Rohlf (1962), para medir el grado en que el fenograma representa
los valores de la matriz de similitud, construyendo, a partir de los valores
del fenograma, una matriz cofenética de similitud, cuyos elementos se definen
como aquellos que determina la proximidad entre los elementos i y j cuando
estos se unen en un mismo clúster. Este coeficiente es la correlación entre los
elementos de la matriz de similitud y la matriz cofenética.
Índice de
consenso: Se utilizó el
índice de consenso Clc para la comparación de los dendrogramas obtenidos,
proveyendo una estimación relativa de la similitud entre los mismos (Rohlf,
1997). Se obtuvo dividiendo el número de ramificaciones en común en los
dendrogramas, entre el número máximo posible de ramificaciones. El valor del
índice varía desde 0 donde no existe ningún consenso hasta 1 donde los
dendrogramas son idénticos (Alagón & Rosas, 2008).
Iniciadores AFLP
Cuatro combinaciones de
iniciadores fueron aplicadas en toda la población, generando un total de 198
bandas, de las cuales 66 fueron polimórficas, representando el 33,33%. (Tabla
1). La combinación de iniciadores con la que se obtuvo mayor número de bandas
fue [E33/M50] con 58 bandas, además, también generó el mayor número de bandas
polimórficas por combinación, que fueron 21 bandas, representando el 36,20%; no
obstante, la combinación con la que se obtuvo mayor porcentaje de bandas polimórficas
fue [E33/M31] (38,46%).
La combinación de
iniciadores con la que se obtuvo mayor número de bandas fue [E33/M50] con 58
bandas, además, también generó el mayor número de bandas polimórficas por
combinación, que fueron 21 bandas, representando el 36,20%; no obstante, la
combinación con la que se obtuvo mayor porcentaje de bandas polimórficas fue
[E33/M31] (38,46%).
Análisis de similitud
genética
La representación del
agrupamiento de las 48 entradas de tarwi según los coeficientes de similitud
Simple Matching (SM) (Figura 1), Jaccard (Figura 2) y Dice (Figura 3),
demuestran diferentes grados de similitud.
Dendrograma
empleando el coeficiente de similitud de Simple Matching
El coeficiente de Simple
Matching evidencia la separación de las 48 accesiones en dos grupos (A y B) a
un nivel de similitud de 0,68. (Figura 1). El grupo A agrupa 43 accesiones,
encontrándose 5 subgrupos dentro de este grupo (i, ii, iii, iv, v) las mismas q
se separan a un nivel de similitud de 0,76. El grupo B agrupa las 5 accesiones
restantes, dividiéndose a un nivel de similitud de 0,71.
Tabla 1
Patrón
de Fragmentos Polimórficos y Valores del Índice de Contenido Polimórfico (PIC)
para las cuatro combinaciones de iniciadores elegidas
|
Iniciadores
EcoRI
|
Iniciadores
MseI
|
Código
|
Fragmentos
Polimórficos
|
N°
Total de Fragmentos
|
%
Polimorfismo
|
|
EcoRI
– AAG
|
MseI
– CAT
|
E33/M50
|
21
|
58
|
36,20
|
|
EcoRI
– ACA
|
MseI
– CAC
|
E35/M48
|
13
|
48
|
27,08
|
|
EcoRI
– AAG
|
MseI
– AAA
|
E33/M31
|
15
|
39
|
38,46
|
|
EcoRI
– AGG
|
MseI
– CAC
|
E41/M48
|
17
|
53
|
32,08
|
|
Promedio
|
16,5
|
49,5
|
33,46
|
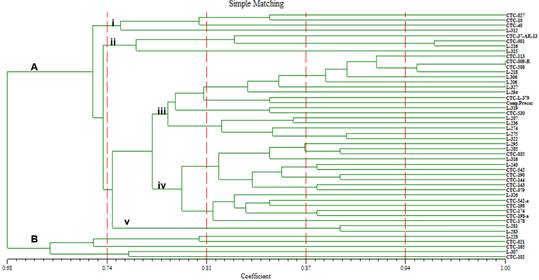
Figura 1. Dendrograma
obtenido mediante el coeficiente de Simple Matching.
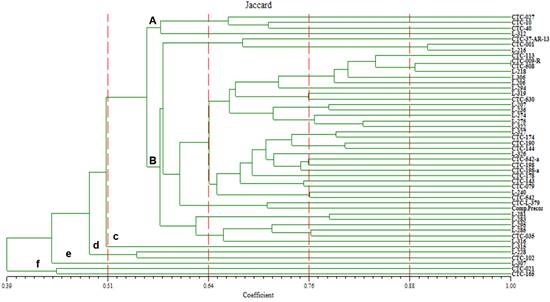
Figura 2. Dendrograma obtenido
mediante el coeficiente de Jaccard.
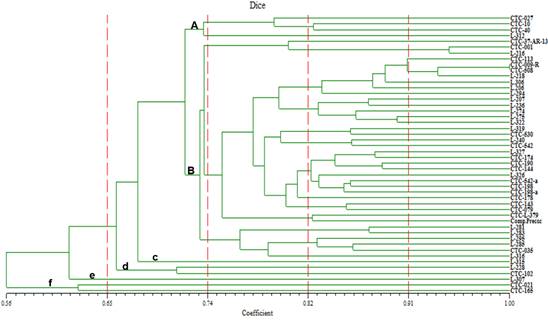
Figura 3. Dendrograma obtenido mediante el coeficiente de
Dice.
Dendrograma
empleando el coeficiente de similitud de Jaccard
La inspección visual del
dendrograma del coeficiente de similitud de Jaccard evidencia una separación en
dos grupos A y B a un nivel de similitud de 0,57. Además, se observan 4 grupos
independientes (c, d, e, f) (Figura 2). En el grupo A se agrupan 4 accesiones,
las mismas que con el coeficiente de Simple Matrching se agrupan en el subgrupo
i del grupo A. En el grupo B se agrupan 38 accesiones en 5 subgrupos (i, ii,
iii, iv, v). En los grupos independientes c y e encontramos una sola accesión,
mientras que en d y f se agrupan dos accesiones.
Dendrograma
empleando el coeficiente de similitud de Dice
Este coeficiente nos
muestra las accesiones agrupadas en dos grupos principales A y B y cuatro
grupos independientes c, d, e y f (Figura 3). Los grupos A y B se separan a un
nivel de similitud de 0,71. El grupo A agrupa las mismas 4 accesiones que el
grupo A del coeficiente de Jaccard. El grupo B agrupa las 38 accesiones que
también agrupa el grupo B del dendrograma del coeficiente de Jaccard. La
distribución de los grupos indepen-dientes c, d, e y f es idéntica a la
observada mediante el coeficiente de Jaccard, diferenciándose en el nivel de
similitud.
Coeficiente de correlación
cofenética (r)
Generadas las matrices de
similitud originales, fueron evaluadas independientemente para obtener las
matrices cofenéticas correspondientes, las mismas que resultaron de un análisis
cofenético partiendo del dendrograma generado con cada coeficiente de similitud
(Tabla 2).
La concordancia entre la
matriz de similitud original y la matriz cofenética (obtenida a partir del
dendrograma), sirvió para evaluar la existencia de diferencias significativas
en la correlación de las mismas, dando como resultado valores “r” del
coeficiente de correlación cofenética que permitieron determinar el coeficiente
de similitud con menor distorsión en su representación a través de su
respectivo dendrograma.
Según Sokal & Sneath
(1973) los valores “r” del coeficiente cofenético, oscilan entre 0,6 y 0,95
entendiéndose los más altos valores como indicadores de una buena
correspondencia entre la matriz original y su representación a través de un
dendrograma. Sin embargo, valores bajos de esta correlación no necesariamente
indican que el dendrograma obtenido no sea de utilidad, sino que solamente
estaría indicando algún tipo de distorsión al momento de obtener el dendrograma
(Rohlf, 1982).
En el presente estudio, el
agrupamiento mediante el coeficiente de Simple Matching demostró el menor grado
de correspondencia (r = 0,68) entre los tres coeficientes de similitud
utilizados, en tanto, los coeficientes de Jaccard y Dice arrojaron valores de
0,79116 y 0,79332 respectivamente. Esto nos indica una menor distorsión en las
relaciones originales existentes entre los elementos en estudio mediante la
representación de la matriz de similitud de Dice.
Índice de consenso (CIc)
El Índice de Consenso (CIc)
indica la similitud entre los dendrogramas obtenidos a través de los
coeficientes de similitud Simple Matching, Jaccard y Dice (Tabla 2), los que se
usaron para agrupar las 48 accesiones de L. mutabilis Sweet usadas en el
presente estudio.
Según Meyer et al. (2004) y
Dalirsefat et al. (2009) la comparación a través del índice de consenso (CIc)
de los dendrogramas obtenidos, permite el refinamiento de aquello apreciado
mediante la inspección visual. Este índice cuya amplitud va de 0 a 1, considera
idénticos dos dendrogramas cuando el valor calculado es uno. Como se muestra en
la tabla 2, el índice de consenso entre los coeficientes de Jaccard y Dice
(0,93) es muy cercano a uno, evidenciándose en la idéntica distribución de los
grupos, variando solo el nivel de similitud. Los valores CIc para SM – J y SM –
D (0,52), demuestran una baja similaridad entre esos dendrogramas, evidenciado
en la diferente distribución de los grupos, así como en los niveles de
similitud.
La similar apariencia,
basada en los dendrogramas, de los coeficientes Jaccard y Dice se puede
simplificar en las propiedades de estos. Se distinguen por la forma como estos
emplean la matriz de datos original (1 = presencia de marcador AFLP y 0 =
ausencia) en la estimación de similitud. Es así que Jaccard y Dice son
equivalentes, excepto que Dice le brinda doble valor a las co-ocurrencias
positivas, mientras que Simple Matching es el único que toma en cuenta las
co-ocurrencias negativas (Duarte et al., 1999).
Elección del coeficiente de
similitud
La selección del
coeficiente de similitud que se tomó en cuenta para los posteriores análisis de
agrupamientos estuvo en función de las propiedades intrínsecas de cada
coeficiente, del nivel de similitud obtenido con cada coeficiente (Tabla 2), de
la ploidía del organismo analizado que es la especie Lupinus mutabilis
Sweet y de la base teórica correspondiente al marcador molecular utilizado, en
este caso AFLP.
Tabla 2
Coeficientes de similitud y
su respectivo coeficiente de correlación cofenética. Nivel de similitud e
índice de consenso
|
Coeficiente
de similitud
|
Coeficiente de
correlación cofenética “r”
|
Nivel de similitud
|
Índice de consenso
|
|
Simple
Matching (SM)
|
r
= 0,68674
|
0,68
|
SM
– J
|
0,52
|
|
Jaccard
(J)
|
r
= 0,79116
|
0,39
|
SM
– D
|
0,52
|
|
Dice
(D)
|
r
= 0,79332
|
0,56
|
J
- D
|
0,93
|
En la Tabla 2 se observa
que el coeficiente SM es el que mayor nivel de similitud evidencia (0,68),
corroborando que, para un conjunto dado de datos, los valores correspondientes
de similitud de Jaccard son siempre menores que los de la similitud de Dice y
los de Simple Matchig. Por otro lado, los valores de la similitud de Dice
pueden ser mayores o menores que los valores correspondientes al coeficiente SM
en función de si el número de posiciones con bandas compartidas es mayor o
menor que el número de posiciones con ausencia compartida de bandas,
respectivamente (Kosman & Leonard, 2005); esto es debido a que el
coeficiente de Dice brinda doble valor a las bandas compartidas (1–1), mientras
que el coeficiente SM considera por igual las dobles ausencias (0-0). Siendo el
nivel de similitud de Dice (0,56) que es menor que el de SM (0,68), se infiere
que existen mayores ausencias compartidas de bandas, posiblemente debido a las
combinaciones de cebadores utilizadas, ya que, tanto EcoRI como MseI contenían
+3 nucleótidos, haciéndose más específica la amplificación, en comparación con
el análisis de Jimenez (2006) que utilizó EcoRI +2 y MseI + 3, obteniendo
mediante el coeficiente de Dice un nivel de similitud que varió de entre 0,81 a
0,98; pues los cebadores con dos nucleótidos selectivos amplifican 1/256 de
fragmentos de restricción y cebadores con tres amplifican 1/4096 de fragmentos
(Weising et al., 2005).
Teniendo en cuenta que la
agrupación y coordinación de los resultados pueden ser influenciadas por la
elección del coeficiente (Duarte et al., 1999), estos coeficientes deben ser
mejor entendidos. El coeficiente de similitud empleado debe reflejar con
precisión nuestro mejor entendimiento del fenotipo observado, así como la base
genética de los individuos estudiados. (Kosman & Leonard, 2005).
Reif et al. (2005)
examinaron 10 coeficientes de similitud ampliamente utilizados en las
evaluaciones de germoplasma, con especial énfasis en aplicaciones en bancos de
cultivo de plantas y semillas. Sugieren el término "alelo
informativo" si las frecuencias alélicas se pueden determinar a partir de
los datos de marcadores moleculares, y el término "alelo no
informativo" si no pueden hacerlo. Entonces, cuando los datos generados
por los marcadores moleculares son "alelos no informativos", como es
el caso de los marcadores dominantes, utilizándose AFLP’s en este estudio, las
estimaciones de los coeficientes entre OTU se pueden calcular por uno de los
tres coeficientes: Simple Matching, Jaccard y Dice, basándose en la ausencia o
presencia de bandas observadas (Sneath & Sokal,1973). El argumento original
para excluir las co-ocurrencias negativas (0-0) está basado en el uso de rasgos
donde todos los grupos que fueron comparados incluyeron el estado 0 del rasgo.
Por un enfoque conservador, la similaridad en las huellas de ADN es
generalmente definida como la fracción de bandas observadas que son compartidas
por dos individuos. Para marcadores dominantes, como los AFLP, generalmente se
asume que cada banda representa un diferente locus bi-alélico (Williams et al.,
1990) y que la alternativa a una banda en la posición característica de ese
locus en el gel, es la ausencia de una banda en cualquier parte del gel.
Además, con estos marcadores, los individuos que son heterocigotos para una
banda de ADN en una posición específica, no pueden distinguirse con certeza de
los individuos que son heterocigotos para esa banda (Kosman & Leonard,
2005).
Según Kosman & Leonard
(2005) el mayor problema en la elección del coeficiente de similitud para
análisis de datos obtenidos con marcadores moleculares dominantes, es el
tratamiento de la ausencia de una banda compartida en alguna posición por dos
individuos. Un argumento común contra el uso del coeficiente SM para datos de
marcadores dominantes es que la ausencia de una banda compartida por dos
individuos no debe considerarse como una prueba de similitud entre ellos. El
fundamento común de este argumento es que la ausencia de un rasgo puede ser
consecuencia de muchas causas diferentes, y por lo tanto la ausencia de
cualquier rasgo compartido no es una buena prueba de similitud genética. Este
argumento, sin embargo, ignora el alto grado de identidad de secuencia de ADN
entre los miembros de una misma especie. Es así, que siendo los individuos aquí
estudiados miembros de una misma especie (L. mutabilis Sweet), si dos de
ellos presentasen una banda en una determinada posición, se asume que son
idénticos en esa región, aparte de la secuencia de nucleótidos correspondientes
a los cebadores utilizados en la amplificación. Por otro lado, ante la ausencia
de banda en la misma posición por parte de otros individuos, podemos inferir
que tienen una altísima probabilidad de poseer una secuencia idéntica en esa
región de ADN, muy aparte de los pares de bases de nucleótidos pertenecientes a
los cebadores, inclusive si provienen de regiones geográficamente separadas.
Un enfoque más conservador
sería suponer, como el coeficiente SM hace, que la falta de una banda
compartida por dos miembros de la misma especie, es una buena evidencia de que
los dos son genéticamente similares en esa región (Kosman & Leonard, 2005);
en ese entender, se ha considerado al igual que Hallden et al. (1994) y Beharav
et al. (2010) que el coeficiente de SM ha de ser la medida más apropiada de
similitud cuando se consideran los taxones estrechamente relacionados.
El
coeficiente de similaridad de Simple Matching es la medida de similitud más
idónea para análisis de variabilidad genética inter e intrapoblacionales de
taxones estrechamente relacionados usando marcadores moleculares de naturaleza
dominante al tomar en cuenta, como un factor de similitud, fragmentos de ADN
ausentes en ambos individuos.
Los
coeficientes de Jaccard y Dice muestran mejores evidencias de similaridad si se
comparan individuos y/o poblaciones con cierta distancia genética, donde la
ausencia compartida de bandas no es asumida como un factor de similitud.
REFERENCIAS
BIBLIOGRÁFICAS
Alagón,
T., & Rosas, R. (2008). Caracterización Molecular de Mashua (Tropelum
tuberosum) de las comunidades campesinas de Cusco y Huánuco (Tesis de
maestría). Universidad Católica de Santa María. Arequipa, Perú.
Atchison,
G., Nevado, B., Eastwood, R., Contreras-Ortiz, N., Reynel, C., Madriñán, S., Filatov,
D., & Hughes, C. (2016). Lost crops of the Incas: Origins of
domestication of the Andean pulse crop tarwi, Lupinus mutabilis. Am.
J. Bot. 103, 1592–1606.
Beharav,
A., Maras, M., Kitner, M., Šuštar-Vozlič, J., Sun, G.L., Doležalová, I.,
Lebeda, A., & Meglič, V. (2010). Comparison of three genetic
similarity coefficients based on dominant markers from predominantly
self-pollinating species. Biologia Planctarum. 54, 54-60.
Bero, S. A., Muda, A.K., Choo, Y.H., Muda, N.A., & Pratama, S.F.
(mayo del 2017). Similarity Measure for Molecular Structure: A Brief Review. Journal of
Physics: Conference Series. The 6th International Conference on Computer
Science and Computational Mathematics (ICCSCM 2017), Langkawi, Malaysia.
Chirinos-Arias,
M., Jimenez, J., & Vilca, L. (2015). Análisis de la variabilidad genética
entre 30 accesiones de tarwi (Lupinus mutabilis Sweet.) usando
marcadores moleculares ISSR. Scientia Agropecuaria. 6(1), 17–30.
Crisci,
J., & López, F. (1983). Introducción a la Teoría y Práctica de la
Taxonomía Numérica. Washington D.C., Estados Unidos: Secretaría General de
la O.E.A.
Dalirsefat,
S., Meyer, A., & Mirhoseini, S. (2009). Comparison of similarity
coefficients used for cluster analysis with amplified fragment length polymorphism
markers in the silkworm, Bombyx mori. Journal of Insect Science. 9.
Duarte,
M. C., Santos, J. B., & Melo, L. C. (1999). Comparison of similarity
coefficients based on RAPD markers in the common bean. Genetics and
Molecular Biology. 22(3), 427-432.
Galek,
R., Sawicka-Sienkiewicz, E., Zalewski, D., Stawinski, S., & Spychala, K.
(2017). Searching for low alkaloid forms in the Andean Lupin (Lupinus
mutabilis) Collection. Czech J. Genet. Plant Breed. 53(2), 55–62.
González-Andrés,
F., & Pita, J. (2001). La caracterización vegetal: Objetivos y enfoques.
Conservación y caracterización de recursos filogenéticos. Valladolid,
España: Publicaciones Instituto Nacional de Educación Agrícola.
Gresta,
F., Wink, M., Prins, U., Abberton, M., Capraro, J., Scarafoni, A., & Hill,
G. (2017). Lupins in European cropping systems. Legumes in Cropping Systems,
88-108.
Guilengue,
N., Alves, S., Talhinhas, P., & Neves-Martins, J. (2020). Genetic and
Genomic Diversity in a Tarwi (Lupinus mutabilis Sweet) Germplasm
Collection and Adaptability to Mediterranean Climate Conditions. Agronomy. 10, 21.
Gulisano,
A., Alves, S., Martins, J.N., & Trindade, L.M. (2019). Genetics and
Breeding of Lupinus mutabilis: An Emerging Protein Crop. Front. Plant Sci.
10, 1385.
Hallden,
C., Nilson, N., Rading, I., & Sall, T. (1994). Evaluation of RFLP and RAPD
markers in a comparison of Brassica napus bredding lines. Theoretical
and Applied Genetics. 88, 123-128.
Jaccard,
P. (1912). The distribution of the flora in the alphine zone. New Phytol. 10(2),
37–50.
Jimenez,
J. (2006). Biodiversity of traditional seed propagated crops cultivated in Peruvian
highland. (Tesis doctoral). University of Silesia. Silesia, Polonia.
Kosman,
E., & Leonard, K. (2005). Similarity coefficients for molecular markers in
studies of genetic relationships between individuals for haploid, diploid, and
polyploid species. Molecular Ecology. 14, 415–424.
Loh,
C. S., Li, I. H., & Sheng, Y. (2016). Comparison of similarity measures to
differentiate players’ actions and decision-making profiles in serious games
analytics. Comput.
Human Behav. 64, 562-574.
Martínez,
L., Ruivemkamp, G., & Jongerden, J. (2015). Fitomejoramiento y
racionalidad social: los efectos no intencionales de la liberación de una
semilla de lupino (Lupinus mutabilis Sweet) en Ecuador. Antipod. Rev. Antropol.
Arqueol. 26.
Meyer, A.,
Garcia, A., Souza, A., & Souza, C. (2004). Comparison of similarity
coefficients used for cluster analysis with dominant markers in maize (Zea
mays L.). Genetics and Molecular Biology. 27(1), 83-91.
Moscoe,
L.J., & Emshwiller, E. (2015). Diversity of Oxalis tuberosa Molina:
a comparison between AFLP and microsatellite markers. Genetic
resources and crop evolution, 62(3), 335-347.
Quiñones,
R. (2019). Determinación del número cromosómico de 4 ecotipos de tarwi
(Lupinus mutabilis Sweet), Huaraz-2018 (Tesis de pregrado). Universidad Nacional
Santiago Antúnez de Mayolo. Huaraz, Perú.
Reif, J.,
Melchinger, A., & Frisch, M. (2005). Genetical and mathematical
properties of similarity and dissimilarity coefficients applied in plant
breeding and seed bank management. Crop Sci. 45, 1-7.
Remón-Gamboa,
Y. K., & Peña-Rojas, G. (2018). Diversidad genética de papas nativas (Solanum
spp.) del distrito de Vilcashuamán, Ayacucho-Perú, mediante AFLP. Revista peruana
de biología 25(3), 259-266.
Rohlf,
F. J. (1997). tpsRelw: relative warps analysis. Dept. of Ecology and Evolution,
State Univ. of New York at Stony Brook, Stony Brook, NY.
Rohlf,
F. J. 1982. Consensus indices for comparing classifications. Math. Biosci.
59, 131-144.
Sneath, P. H., & Sokal,
R. R. (1973). Numerical taxonomy the principles and practice of numerical
classification. 1st Edition, San Francisco, Estados Unidos: W. H. Freeman.
Sokal,
R., & Rohlf, F.J. (1962). The comparison of dendrograms by objective methods.
Taxon. 11(2), 33-40.
Suárez-Contreras,
L. (2018). Diversidad genética de Moniliophthora roreri mediante
Polimorfismo de Longitud de Fragmentos Amplificados (AFLPs). Revista
Colombiana De Ciencias Hortícolas. 11(2), 425-434.
Vos, P.,
Hogers, R., Bleeker, M., Reijans, M., Lee, T.A.J., Hornes, M., Frijters, A.,
Pot, J., Peleman, J., & Kuiper, M. (1995). AFLP: a new technique for
DNA fingerprinting. Nucleic Acids Research. 23(21), 4407-4414.
Wang,
J., Lu, H.O.U., Wang, R.Y., He, M.M., & Liu, Q.C. (2017). Genetic diversity
and population structure of 288 potato (Solanum tuberosum L.) germplasms
revealed by SSR and AFLP markers. Journal of Integrative Agriculture. 16(11),
2434-2443.
Weising,
K., Nybom, H., Pfenninger, M., Wolff, K., & Kahl, G. (2005). DNA
fingerprinting in Plants. Principles, Methods and Applications. Florida,
Estados Unidos: Taylor and Francis Group.
Williams,
J. G. K., Kubelik, A. R., Livak, K. J., Rafalski, J. A., & Tingey, S. V.
(1990). DNA polymorphism amplified by arbitrary primers are useful as genetic
markers. Nucleic
Acids Res. 18, 6531-6535.
![]() https://orcid.org/0000-0002-3350-0947 M.M.
Quispe-Flores:
https://orcid.org/0000-0002-3350-0947 M.M.
Quispe-Flores: ![]() https://orcid.org/0000-0003-2682-6188
https://orcid.org/0000-0003-2682-6188 ![]() https://orcid.org/0000-0001-9988-4827
https://orcid.org/0000-0001-9988-4827 

