Aporte de
agua del río “Tres ríos”, según el caudal recesivo, para los años hidrológicos
2008-2015, Cajamarca, Perú
Water
contribution of the “Tres Ríos” River, according to the recessive flow, for the
hydrological years 2008-2015, Cajamarca, Peru
Jairo Isaí Alvarez
Villanueva1,*; José Francisco Huamán Vidaurre1
1
Universidad Nacional de Cajamarca, Facultad de Ingeniería, Av. Atahualpa
Nº 1050.
*Autor corresponsal: jialvarezv@unc.edu.pe (J. I. Alvarez
Villanueva).
ID
ORCID de los autores
Jairo
Isaí Alvarez Villanueva: 
https://orcid.org/0000-0001-8777-3943
José
Francisco Huamán Vidaurre: https://orcid.org/0000-0002-4896-0479
RESUMEN
El objetivo del estudio fue cuantificar el aporte
de agua del río “Tres Ríos” de la microcuenca del mismo nombre. Se utilizaron
dos modelos matemáticos para caudales base: Maillet (1905) y Boussinesq (1904).
Se identificó la curva de agotamiento a partir del segundo punto de quiebre,
con información hidrométrica del período 2008-2015, obtenida en la captación
derivadora Ronquillo ubicada en dicho río. Los caudales simulados fueron
contrastados con los caudales observados del río “Tres Ríos” mediante los siguientes
indicadores estadísticos: Nash-Sutcliffe (0,71), Error Estándar de Estimación
(0,034), Índice de Willmott Modificado (0,70) y una prueba estadística
paramétrica (T Student). Se determinó que el modelo de Maillet (1904) no generó
caudales de agotamiento próximos a los caudales observados del río “Tres Ríos”;
sin embargo, el modelo Boussinesq (1904) generó caudales de agotamiento
subestimados más próximos a los caudales observados. Con el modelo Boussinesq
(1904) se generó caudales de agotamiento medios mensuales y se estimó el aporte
de agua en la captación Ronquillo de la microcuenca obteniéndose un volumen
promedio mensual 4,31 MMC.
Palabras clave: modelo Maillet; modelo Boussinesq;
caudales recesivos; curva de agotamiento.
ABSTRACT
The objective of the study
was to quantify the contribution of water from the river "Tres Ríos"
of the micro-basin of the same name. There was used two mathematical models:
Maillet (1905) and Boussinesq (1904). The depletion curve was identified from
the second break point, with hydrometric information since the period 2008 to
2015, it obtained in the Ronquillo diversion catchment to the same river. The
simulated flows were contrasted with the observed flows of the “Tres Ríos”
river, it used the following statistical indicators: Nash-Sutcliffe (0.71),
Standard Error of Estimation (0.034), Modified Willmott Index (0.70) and a
parametric statistical test (T Student). It was determined that the Maillet
model (1904) it did not generate near depletion flows to the observed flows of
the “Tres Ríos” river; however, the Boussinesq model (1904) generated
underestimated depletion flows to the observed flows. With the Boussinesq model
(1904), the average monthly depletion flows were generated and the contribution
of water in the Ronquillo catchment of the micro-basin was estimated, it
obtained an average monthly volume of 4.31 MMC.
Keywords: Maillet model;
Boussinesq model; recessive flows; depletion curve.
Recibido: 05-01-2022.
Aceptado: 26-02-2022.
El cambio climático tiene impacto en los cambios
de patrones de precipitaciones (El Bilali et al., 2020). La ausencia prolongada de
lluvias se ve reflejada en el desabastecimiento de agua en la ciudad de
Cajamarca, desde hace más de una década. Cuantificar los recursos hídricos
tanto superficiales como subterráneos permitirán realizar planificaciones para
la población cajamarquina en el futuro, frente al crecimiento poblacional. El
propósito de la investigación es determinar el aporte de agua del río “Tres
Ríos” mediante el uso de modelos matemáticos, ya que hasta la fecha no se ha
realizado estudios para determinar el aporte de agua del río “Tres Ríos” en
épocas de estiaje. Pizarro-Tapia et al. (2013), Caro (2001) y Balocchi
(2008) y otros, realizaron investigaciones para determinar el aporte de
caudales recesivos mediante el uso de modelos matemáticos de la forma
exponencial y potencial para diferentes ríos en Chile. La investigación permite
dar a conocer a la población cajamarquina el aporte disponible de agua dulce
del río “Tres Ríos” para uso poblacional en épocas de estiaje. Asimismo, da a
conocer el estado real del caudal circulante en épocas de estiaje del río “Tres
Rìos” de la microcuenca “Tres Ríos”, cuya superficie forma parte de la cabecera
de la gran cuenca del “Amazonas”. Los objetivos del estudio son: determinar el
coeficiente de agotamiento de la microcuenca “Tres Ríos”. Determinar el aporte
de agua o del río “Tres ríos” ajustando un modelo matemático a los caudales
circulantes del río en estudio para períodos de estiaje. La investigación
utilizó herramientas de modelamiento matemático para contribuir a la gestión
del recurso hídrico.
Ubicación
La microcuenca “Tres Ríos”
pertenece a la vertiente del Atlántico, forma parte de la cabecera de la cuenca
del “Amazonas”, ubicada al norte del Perú, en la Región, Departamento,
Provincia y Distrito de Cajamarca (Figura 1). Sus aguas descargan en los ríos
“Cajamarquino”, “Marañón” y al caudaloso río “Amazonas”. La microcuenca “Tres
Ríos”, se encuentra ubicada en la longitud oeste (78032´11,99”) y latitud sur
(7032`11,99”).
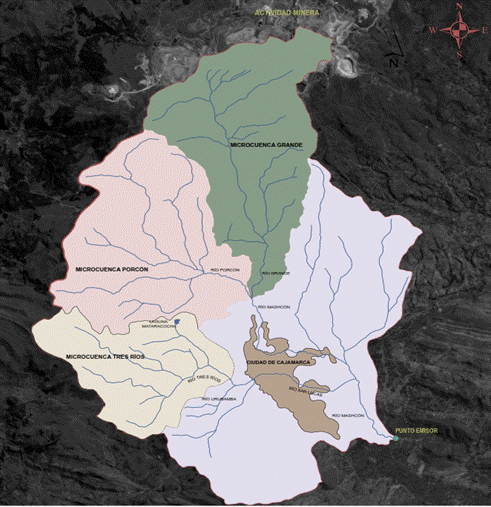
Figura 1. Principales microcuencas de la cuenca
Mashcón, Cajamarca, Perú.
La microcuenca presenta un área
de 41,5 km2. Su elevación está entre los 2840 m.s.n.m y 3950
m.s.n.m, y su perímetro es de 31,8 km. Además, está formada por subcuencas,
estas son: subcuenca “Balconcillo”, subcuenca “Manzana”, subcuenca “Coshunga” y
subcuenca “Tres ríos”. El principal río de la microcuenca, es el río “Tres Ríos”,
presenta característica de alta montaña, presenta una escorrentía de tipo
perenne el cual varia en los meses de mayo a septiembre. El principal uso de
sus aguas está destinado para uso población, y son captadas en la captación
Ronquillo por la Empresa Prestadora de Servicios de Saneamiento de Cajamarca
(Eps Sedacaj S.A). En la Figura 1 se observan las tres microcuencas más
importantes para el abastecimiento de agua para la ciudad de Cajamarca, estas
son: Microcuenca “Tres Ríos”, “Porcòn” y “Grande”.
Información requerida
La información de caudales par el estudio fue de
35 datos, obtenidos de la estación hidrométrica “Ronquillo” del período 2008 –
2015. Pertenece a la Escuela Académica Profesional de Ingeniería Hidráulica,
instalada en propiedad de la Eps Sedacaj S.A. La estación hidrométrica registra
mediciones diarias cada 15min de cotas en (m) y caudales en (m3/s).
Los caudales de agua que la Eps Sedacaj S.A capta del río “Tres Ríos” hacia
planta de tratamiento de agua potable “San Apolonia”, fueron obtenida del
Boletín diario de control de procesos. La información recopilada de caudales,
fue evaluada para detectar outliers, a través del método de análisis de datos
dudosos propuesto por Chow et al (1994). Además, se realizó un análisis gráfico
para verificar si existen saltos o vacíos en la información, así como un
análisis de consistencia.
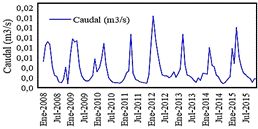
Figura 2. Registro de
caudales medios mensuales del río “Tres Ríos”, período 2008-2015.
Fórmulas empleadas
En la Tabla1 se presentan las
fórmulas de los modelos de Maillet (1905) y Boussinesq (1904). A partir de
estas fórmulas se derivan otras fórmulas tal como presentan a continuación (Maillet, 1905):
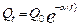(1)
Boussinesq (1904)
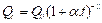(2)
Fórmulas de coeficiente de agotamiento, derivados
de la fórmula 1 y 2. Donde: Q0 > Qt.
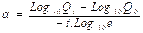(3)
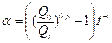(4)
Fórmulas de almacenamiento, obtenidas por
integración de las Fórmulas 1 y 2 (Samper, 2014).
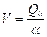(5)
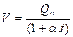(6)
Según Balocchi et al. (2014) y Pizarro-Tapia et al. (2013), Qt:
representa el caudal en el tiempo t (m3s-1); Q0:
caudal inicial de recesión (m3s-1); α: coeficiente
de agotamiento (día-1); t: tiempo de recesión (día); V: Volumen
de almacenamiento (MMC); y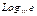
: 0,4343, 
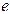=2,71828.
Inicio de la curva de agotamiento
En el análisis del hidrograma, se identificó el
punto de inicio de las aguas subterráneas del período 2008 - 2015,
identificando de esta manera a los meses de estiaje (mayo-septiembre). Para
ello se utilizó el método de Pizarro (1993), utilizado por Balocchi et al. (2014)
quienes indicaron, que el inicio del caudal recesivo empieza en el segundo
punto de quiebre de curva de descenso del hidrograma, el cual está representado
como puntos de quiebres o puntos de inflexión. Además, señala que este punto es
el inicio de caudales de origen subterráneo y el inicio de los caudales
recesivos. La distribución de la curva de agotamiento adquiere una gráfica
lineal, cuando se grafique el logaritmo del caudal observado de la curva de
agotamiento del hidrograma (Q) versus tiempo (t).
Coeficientes de agotamiento
Conociendo el inicio de la curva recesiva o de
agotamiento, es posible obtener el coeficiente de agotamiento (α),
mediante la selección de dos caudales distintos (caudal inicial Q0,
caudal final Qt) y la selección de un determinado tiempo (t) en días (Pizarro-Tapia et al.,
2013). Manga
(2001) señala que los caudales recesivos son utilizados para entender el
comportamiento del sistema de aguas subterráneas. Para obtener los distintos
coeficientes de agotamientos (α) de cada mes de estiaje del período
2008-2015, se utilizó las Fórmulas 3 y 4. Se determinó los valores máximos y
mínimos del coeficiente de agotamiento para cada modelo (Fórmula 1 y 2), y en
base a los promedios de los coeficientes de agotamiento del período de estiaje
2008-2015, se logró establecer un valor que logró calibrar a los modelos (Fórmula
1 y 2), y de esta manera lograr conocer el comportamiento de las reservas de
agua en los acuíferos. Custodio y Llamas (1996) señala que este valor permitirá
determinar el volumen de almacenamiento de aguas subterráneas, para ello se usó
las Fórmula 5 y 6. Asimismo, este valor cumplió con la condición de Maillet
(1905), es decir, que este coeficiente sea mayor a cero.
Calibración y Simulación
Identificados los meses de estiajes y los tiempos
de duración, se procedió identificar un valor dentro del rango de valores
máximos y mínimos de coeficiente de agotamiento para cada modelo de la Fórmula
1 y 2. La calibración inició tomado al promedio del coeficiente de agotamiento
hasta lograr ajustarse a los caudales recesivos del río “Tres Ríos”, siguiendo
lo establecido por Erasun et al.
(2018) quien indica que un
tipo de calibración es el de “prueba y error”. Para la simulación se
utilizó los modelos de Maillet (1905) Boussinesq (1904), ver Fórmulas 1 y 2.
Validación
Para
la validación se utilizó indicadores estadísti-cos (Tabla 1), estos presentan
una métrica de rangos establecidos para determinar la eficiencia de la
simulación de los modelos (Fórmula 1 y 2).
Tabla 1
Métrica
de evaluación de indicadores estadísticos
|
Indicador
|
Rango
|
Valor ideal
|
|
NS
|
[-α;1]
|
1
|
|
IWM
|
[0;1]
|
1
|
|
EEE
|
[0;
+α]
|
0
|
Fuente:
(Moncada & Willems,
2020.).
Nota:
Nash-Sutcliffe (NS), Error Estándar de Estimación (EEE), Índice de Willmott Modificado
(IWM).
Comparación de muestras
Los caudales recesivos simulados fueron contras-tados
con los caudales observados del río “Tres Ríos”, esto permitió plantear las
siguientes hipótesis: Hipótesis nula, H0: No hay diferencias entre
la media de las muestras observadas y simuladas. Sí, P-Valor> “a” entonces
se acepta la hipótesis nula. Hipótesis Alternativa, H1: Hay
diferencias entre la media de las muestras observadas y simuladas. Sí, P-Valor
< “a” entonces se acepta la hipótesis alternativa. Para realizar la
comparación entre ambas variables primero se realizó una prueba de normalidad,
para establecer si las pruebas (paramétricas, no paramétricas) pueden responder
a las hipótesis planteadas.
Volumen de almacenamiento
Validado finalmente el modelo Boussinesq (1904), y
conociendo las variables de entrada para cada modelo (Fórmula 6) tales como:
caudal recesivo observado inicial, coeficiente de agotamiento y un lapso de
tiempo en días, se simuló la Fórmula 6 y se determinó el volumen de
almacenamiento.
En la Tabla 2 están identificados los caudales
recesivos en m3/s, los meses de estiaje, y los meses de inicio de
los caudales recesivos. Para este análisis se sumó a los caudales registrados
por la
estación hidrométrica Ronquillo, el caudal
promedio de 65 l/s, captado por la Eps Sedacaj S.A, en la captación Ronquillo. El inicio del caudal recesivo (Tabla 2)
fue tomado a partir del segundo punto de quiebre de la curva de descenso del
hidrograma, el cual está relacionado con el inicio de aporte exclusivamente de
agua subterránea. (Balocchi et al., 2014a).
La Tabla 3 presenta
los coeficientes de agotamiento (α) calibrados mediante el método prueba y
error, se utilizó criterios deductivos y observaciones para obtener los
coeficientes de agotamiento (α) calibrados (Tabla 3). Se tuvo en cuenta el
rango de valores de coeficiente de agotamiento 0.0001 < α < 0.018
(día-1). Esto involucró hacer ajustes manuales para lograr la
eficiencia de simulación de los modelos (Fórmula 1 y 2). Gómez y Gómez (2016)
indica que a medida que avanzan los meses de estiaje el coeficiente de
agotamiento va reduciéndose. Coincidiendo con Balocchi et al. (2014a) quien
afirma que este valor va disminuyendo a medida que avanza el tiempo. Asimismo,
señala que este valor representa la pendiente de la curva de descenso de la
curva de agotamiento. El coeficiente de agotamiento calibrado para la
investigación fue de 0,003 día-1 (Tabla 3). Maillet (1905) sostiene
que este valor tiene que ser mayor a cero, lo cual cumple con esa condición. El
resultado se compara con los coeficientes de agotamiento tales como: 0,027 día-1
y 0,08 día-1 calculados por Adarve, Fedeli y Castillo (1998) los
cuales indican un rápido agotamiento y una elevada conductividad hidráulica.
Tabla 2
Caudales
recesivos del río “Tres Ríos”
|
Año
|
Meses de estiaje,
2008-2015
|
|
2008
|
Jun-2008
|
Jul-2008
|
Ago-2008
|
Set-2008
|
|
|
|
Q (m3/s)
|
0,267
|
0,197
|
0,154
|
0,125
|
|
|
|
2009
|
Jun-2009
|
Jul-2009
|
Ago-2009
|
|
|
|
|
Q (m3/s)
|
0,220
|
0,159
|
0,133
|
|
|
|
|
2010
|
Jun-2010
|
Jul-2010
|
Ago-2010
|
Set-2010
|
|
|
|
Q (m3/s)
|
0,187
|
0,167
|
0,142
|
0,120
|
|
|
|
2011
|
Jun-2011
|
Jul-2011
|
Ago-2011
|
Set-2011
|
Oct-2011
|
Nov-2011
|
|
Q (m3/s)
|
0,271
|
0,211
|
0,210
|
0,168
|
0,152
|
0,123
|
|
2012
|
May-2012
|
Jun-2012
|
Jul-2012
|
Ago-2012
|
|
|
|
Q (m3/s)
|
0,242
|
0,217
|
0,173
|
0,099
|
|
|
|
2013
|
May-2013
|
Jun-2013
|
Jul-2013
|
Ago-2013
|
Set-2013
|
|
|
Q (m3/s)
|
0,273
|
0,261
|
0,234
|
0,162
|
0,132
|
|
|
2014
|
Jun-2014
|
Jul-2014
|
Ago-2014
|
Set-2014
|
|
|
|
Q (m3/s)
|
0,300
|
0,269
|
0,166
|
0,125
|
|
|
|
2015
|
Jun-2015
|
Jul-2015
|
Ago-2015
|
Set-2015
|
Oct-2015
|
|
|
Q (m3/s)
|
0,331
|
0,298
|
0,264
|
0,221
|
0,144
|
|
Por otro lado, Pulido
(1979) señala que valores de 0,023 día-1 y 0,116 día-1,
indican un vaciado rápido de agua subterránea. Asimismo, Liñán (2005) señala
que con valores de orden de 10-3 día-1 en zonas
karstificadas indicarían un agotamiento de manera lenta, por presentarse en una
zona saturada y por ende una descarga lenta. Como el coeficiente de agotamiento
de la investigación se encuentra en el orden de 10-3 entonces
podemos señalar que las descargas de las aguas subterráneas son lentas o
reguladas de forma natural. Del resultado se señala que mientras mayor sea el
valor del coeficiente de agotamiento, existirá un vaciado rápido de agua
subterránea. Posteriormente,
se procedió a simular los modelos (Fórmulas 1 y 2) utilizando la información de
la Tabla 3 y a validar un modelo que mejor se ajuste a los caudales recesivos
del río “Tres Ríos”.
Tabla 3
Coeficientes de agotamiento calibrados
|
Modelo
|
Coeficiente
de agotamiento
|
|
Maillet
(1905)
|
0,006 día-1
|
|
Boussinesq
(1904)
|
0,003 día-1
|
La Tabla 4 muestra que los caudales
simulados por el modelo de Boussinesq
(1904), presentaron los mejores resultados de indicadores estadísticos frente a
los resultados de Maillet (1905), Moncada y Willems, (2020) señalan que
el grado de confiabilidad del modelo se obtiene mediante la eficiencia dada por
los indicadores estadísticos. El modelo no presenta un ajuste perfecto debido a
que el NS es menor a 1(Moncada
& Willems, 2020). No es excelente por ser NS menor a 0, 8. El modelo es
bueno por estar dentro del rango de 0,6-0,8. Según el indacador IWM el modelo
no hace una ajuste perfecto por ser menor a 1 (Moncada & Willems, 2020). Para EEE un valor de 0
indica que los valores simulados son óptimos (Wijayarathne y Coulibaly, 2020).
Tabla 4
Resultado de indicadores estadísticos
|
Indicadores
|
Valor ideal
|
Maillet
(1905)
|
Boussinesq
(1904)
|
|
NS
|
1
|
0,67
|
0,71
|
|
IWM
|
1
|
0,68
|
0,70
|
|
EEE
|
0
|
0,036
|
0,034
|
Los caudales recesivos simulados por el modelo de
Boussinesq (1904) fueron contrastados con los caudales observados del río “Tres
Ríos”, permitiendo realizar la prueba de distribución Normal mediante la prueba
de Shapiro Wilk, se demostró que dicha relación presenta una distribución
normal por tanto se eligió la prueba de T Student con un nivel de significación
(“a”= 0,05), Esta prueba logró comparar la media de las muestras relacionadas.
Se determinó que P-valor < 0,05,
por tanto, se acepta la hipótesis alternativa. Demostrando que existe
una sub estimación en la simulación. Una subestimación de caudales Caro (2001)
señala que es más beneficiosa que una sobreestimación, puesto que permitiría
realizar una planificación mucho más racional en el uso de los caudales en
meses de ausencia de lluvias.
Tabla 5
Volúmenes de agua en épocas de estiaje, 2008-2015
|
Meses
de estiaje
|
Año
|
Volumen simulado de río
(MMC)
|
|
Junio-
septiembre
|
2008
|
4,10
|
|
Junio-
agosto
|
2009
|
3,76
|
|
Junio-
septiembre
|
2010
|
3,40
|
|
Junio-
noviembre
|
2011
|
4,17
|
|
Mayo-
agosto
|
2012
|
4,03
|
|
Mayo-
septiembre
|
2013
|
4,69
|
|
Junio-septiembre
|
2014
|
4,76
|
|
Junio-octubre
|
2015
|
5,56
|
|
Volumen
promedio de caudales simulados
|
4,30
|
|
Volumen
promedio de caudales observados
|
5,21
|
El aporte de agua de la microcuenca “Tres Ríos” en
períodos de estiaje, se obtuvo mediante el volumen promedio mensual para los
meses de estiaje, del período 2008-2015, mediante la Fórmula 6. La Tabla 5 presenta una
subestimación entre los promedios de los volúmenes simulados y los observados
para el período 2008-2015.
Según Caro (2001) una subestimación permitirá hacer una planificación muy
racional en el uso del agua. Remenieras (1974) y Custodio y Llamas (1976)
coinciden en que estos volúmenes de almacenamiento de origen subterráneo en
épocas de estiaje, son las reservas subterráneas de una cuenca y que según
Condon et al. (2020) está en función de la capacidad de recarga de las fuentes
naturales por acción de lluvias. Finalmente,
Jodar-Abellan et al. (2018) señala que los modelos hidrológicos son
herramientas que permiten planificar, gestionar sosteniblemente el recurso
hídrico.
Los modelos de Maillet (1905) y Boussinesq (1904) son
los más comunes para simular caudales recesivos. El modelo de Boussinesq (1904)
fue validado para simular caudales recesivos en la microcuenca “Tres Ríos”. Se
utilizó la Fórmula 6 para cuantificar el aporte de agua del río “Tres ríos” en
épocas de estiaje, obteniendo de esta manera un volumen promedio mensual de
4,313 MMC para el período 2008-2015. Este valor representa el volumen de
almacenamiento de agua subterránea liberada por los acuíferos de la microcuenca
“Tres Ríos” en épocas de estiaje. Además, esta información será base para la
planificación del recurso hídrico para la ciudad de Cajamarca, frente al cambio
climático y al acelerado crecimiento poblacional.
REFERENCIAS
BIBLIOGRÁFICAS
Adarve, A.,
Castillo, A., & Fedeli, B. (1998). Análisis de curvas de agotamiento en dos
ríos de Sierra Nevada (Granada, España). Universidad de Granada, España.
Balocchi, F.
(2008). Modelación de caudales recesivos para períodos estivales en la cuenca
del Estero Upeo, Región del Maule.
Balocchi,
F., Pizarro, R., Morales, C., & Olivares, C. (2014), Modelamiento
matemático de caudales recesivos en la región mediterránea andina del Maule: el
caso del estero Upeo, Chile. Tecnología y ciencias del agua, 5(5),
179-188.
Caro, J. A,
(2001). Modelación de caudales recesivos para la cuenca del río Purapel. Estación
Nirivilo.
Condon,
L. E., Markovich, K. H., Kelleher, C. A., McDonnell, J. J., Ferguson, G., &
McIntosh, J. C. (2020). ¿Where is the bottom of a watershed? Water Resources Research,
56, 1-9.
Custodio, M.
E., & Llamas, M. R. (1996). Hidrología Subterránea. Barcelona, España: Omega.
Chow,
V. T., Maidment, D., & Mays, L. (1994). Hidrología aplicada. Bogotá: McGraw Hill.
Erasun,
V., Failache, N., & Gamazo, P. (2018). Modelación hidrológica para la gestión del riesgo
de inundaciones en la cuenca del río Daymán. Congreso Latinoamericano de
Hidráulica. Argentina.
Gómez, S.,
& Gómez, V. L. (2016). Baseflow analysis
using master recession curves and numerical algorithms in mountain basins:
Suratá's river and Oro's river (Santander, Colombia). DYNA, 83(196), 213-222.
Jodar-Abellan,
A., Ruiz, M., & Melgarejo, J. (2018). Evaluación del impacto del cambio
climático sobre una cuenca hidrológica en régimen natural (SE, España) usando
un modelo SWAT. Revista mexicana de ciencias geológicas, 35(3),
240-253.
Liñán, C. (2005). Hidrogeología
de acuíferos carbonatados en la unidad Yunquera-Nieves (Málaga). Instituto
Geológico y Minero de España.
El Bilali, H., Bassole, I.
H. N., Dambo, L., & Berjan, S. (2020). Climate change and food
security. Agriculture and Forestry, 66(3), 197–210.
Manga,
M. (2001). Origin of Post Seismic Stream Flow Changes Inferred from Baseflow
and Magnitude-Distance Relations, Geophysical Research Letters, 28,
2133-2136.
Moncada, W.,
& Willems, B. (2020). Tendencia anual del caudal de salida, comparado con
el caudal ecológico, en la Microcuenca Apacheta/Ayacucho/Perú, 2000 a 2018. Ecología
Aplicada, 19(2), 93-102.
Maillet, E.
(1905). D’Hydrauloque. París, Francia: Librairie Scientifique.
Pizarro-Tapia,
R., Balocchi-Contreras, F., Garcia-Chevesich, P., Macaya-Pérez, K., Bro, P., et
al. (2013).
On Redefining the Onset of Baseflow Recession on Storm Hydrographs. Open Journal of
Modern Hydrology, 3(4), 269–277.
Pulido, A.
(1979). Contribución al conocimiento de la hidrogeología del prebético
nororiental.
Remenieras,
G. (1974). Tratado de la Hidrología Aplicada. Barcelona, España: Técnicos
Asociados.
Samper, J.
(2014). Manantiales y relaciones Río Acuífero de Hidrología del Subsuelo.
Wijayarathne, D. B., & Coulibaly, P. (2020).
Identification of hydrological models for operational flood forecasting in St.
John’s, Newfoundland, Canadá. Journal of Hydrology: Regional Studies, 27,
100646.
