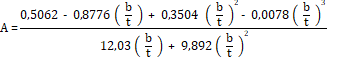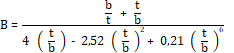Módulo de
rigidez de especies de madera de importancia comercial para México: Pinus
pseudostrobus, Tabebuia rosea y Quercus scytophylla
Modulus of rigidity
of commercially important wood species for Mexico: Pinus pseudostrobus,
Tabebuia rosea and Quercus scytophylla
Javier Ramón Sotomayor
Castellanos 1, *; Isarael Macedo
Alquicira 1; Juan Zárate Medina 1
1 Universidad Michoacana de
San Nicolás de Hidalgo, Ciudad Universitaria, Morelia, México.
* Autor
corresponsal: madera999@yahoo.com (J. R. Sotomayor Castellanos).
ID
ORCID de los autores
J. R. Sotomayor Castellanos:  https://orcid.org/0000-0002-1527-8801 I. Macedo
Alquecira:
https://orcid.org/0000-0002-1527-8801 I. Macedo
Alquecira:  https://orcid.org/0000-0002-6432-6574
https://orcid.org/0000-0002-6432-6574
J.
Zárate Medina:  https://orcid.org/0000-0002-3662-3272
https://orcid.org/0000-0002-3662-3272
RESUMEN
La madera es un material
biológico con aplicaciones en ingeniería y arquitectura. Su módulo de rigidez
es útil para el cálculo de vigas que trabajan en flexión y en torsión. El
objetivo de la investigación fue determinar los módulos de rigidez y los
índices materiales de Pinus pseudostrobus, Tabebuia rosea
y Quercus scytophylla. Se realizaron pruebas dinámicas de torsión
en 35 probetas de pequeñas dimensiones de cada una de las especies. Se
calcularon las correlaciones lineales y sus coeficientes de determinación de
los módulos de rigidez en función de la densidad y de la frecuencia. Los
principales resultados son: Las magnitudes de las densidades de las maderas de P.
pseudostrobus, T. rosea y Q. scytophylla se
ubican al interior del intervalo: 587 kg m-3,
735 kg m-3. El coeficiente de variación de las frecuencias
para Q. scytophylla es 50% menor comparativamente con los coeficientes
de P. pseudostrobus y T. rosea. El coeficiente de
variación para P. pseudostrobus es 23% mayor que el de T. rosea
y 146% mayor que el de Q. scytophylla. Se concluye que los
valores reportados en esta investigación pueden ser útiles si estas especies de
maderas se utilizan con fines estructurales.
Palabras
clave:
ingeniería;
arquitectura; variabilidad de la madera; resistencia mecánica; tamaño de la
muestra.
ABSTRACT
Wood is a biological
material with applications in engineering and architecture. Its modulus of
rigidity is useful for the calculation of beams that work in bending and
torsion. The objective of the research was to determine the rigidity moduli and
material indices of Pinus pseudostrobus, Tabebuia rosea
and Quercus scytophylla. Dynamic torsion tests were performed on 35
small specimens of each species. Linear correlations and their coefficients for
determining the modulus of rigidity as a function of density and frequency were
calculated. The main results are: The magnitudes of the wood densities of P.
pseudostrobus, T. rosea and Q. scytophylla
are located within the interval: 587 kg m-3,
735 kg m-3. The coefficient of variation of the frequencies
for Q. scytophylla is 50% lower compared to the coefficients of P.
pseudostrobus and T. rosea. The coefficient of variation
for P. pseudostrobus is 23% greater than that of T. rosea
and 146% greater than that of Q. scytophylla. It is concluded
that the values reported in this research may be useful if these
wood species are used for structural purposes.
Keywords: engineering; architecture;
wood variability; mechanical strength; sample size.
Recibido: 29-04-2023.
Aceptado: 04-09-2023.

INTRODUCCIÓN
La madera es un material de origen biológico con
amplias aplicaciones en ingeniería y arquitectura (Jacob et al., 2018). Como
consecuencia, las magnitudes de sus propiedades físicas denotan una amplia
variabilidad entre especies, árboles y al interior de un mismo individuo
(Malesza, 2015). Además, las características de resistencia mecánica de una
misma especie varían según la técnica empleada en su determinación (Chauhan &
Sethy, 2016) y el contenido de humedad de la madera (Jaskowska-Lemanska &
Przesmycka, 2020). De tal forma, su caracterización requiere del estudio de
especie por especie.
El módulo de rigidez es útil para el cálculo de
elementos y conexiones donde aparecen deformaciones fuera de plano, ocasionadas
por esfuerzos cortantes; por ejemplo, en vigas que trabajan en flexión y en
torsión, así como en conexiones entre elementos estructurales en edificaciones
y en artículos de madera (Echenique et al., 2015). En el mismo contexto, el
aserrío de madera produce usualmente paralelepípedos para uso estructural,
recortados en el plano radial-tangencial con al menos dos de sus caras
mostrando planos longitudinales-tangenciales. De esta forma, cuando la madera
está en servicio, trabaja como viga en flexión o como elemento resistente en
productos compuestos de madera.
Así, el módulo de rigidez para el plano
longitudinal-tangencial es el parámetro necesario para el diseño de productos
(Brandner et al., 2018) y estructuras de madera (Rocco et al., 2017).
Una de las tendencias contemporáneas en investigación
en ciencias y tecnología de la madera es caracterizar el comportamiento
mecánico de una especie en particular para sugerir su utilización en productos
de valor agregado. Los datos publicados son derivados de experimentos
realizados con probetas con dimensiones específicas de acuerdo con el protocolo
experimental aplicado (Llana et al., 2020). Sin embargo, el utilizador de
piezas de madera en la práctica adquiere piezas de madera aserrada que no
representan necesariamente a la madera observada en condiciones de laboratorio.
En este contexto, existen pocos estudios comparativos de módulos de rigidez de
maderas determinados con diferentes enfoques experimentales. La bibliografía
sobre el tema de investigación es limitada en cuanto al número de trabajos
publicados recientemente. La Tabla 1 presenta una selección de datos
recolectados en la literatura sobre la densidad, el módulo de rigidez y el
índice material de diferentes especies.
Los autores referidos en la Tabla 1
emplean diferentes estrategias para determinar los módulos de rigidez en el
plano longitudinal-tangencial (GLT).
Tabla 1
Datos de densidades, módulos de rigidez de la
bibliografía e índices materiales
|
Especie
|
ρCH
|
GLT
|
Itor*
|
Referencia
|
|
(kg m-3)
|
(MN m-2)
|
|
Paulownia tomentosa
|
300
|
703
|
2,34
|
Komán & Feher (2017)
|
|
Thuja plicata
|
353
|
320
|
0,91
|
Sotomayor & Villaseñor (2016)
|
|
Cryptomeria japonica
|
360
|
784
|
2,18
|
Anshari et al. (2011)
|
|
Picea sitchensis
|
390
|
720
|
1,85
|
Wang et al. (2018)
|
|
Abies balsamea
|
393
|
575
|
1,46
|
Hernández y Sotomayor (2014)
|
|
Pinus sylvestris
|
398
|
755
|
1,90
|
Roohnia & Kohantorabi (2015)
|
|
Picea sitchensis
|
400
|
400
|
1,00
|
Yoshihara (2012)
|
|
Picea abies
|
465
|
863
|
1,86
|
Kránitz et al. (2014)
|
|
Picea abies
|
472
|
744
|
1,58
|
Olsson & Källsner (2013)
|
|
Pinus densiflora
|
510
|
981
|
1,92
|
Cha (2015)
|
|
Pinus pseudostrobus
|
540
|
922
|
1,71
|
Sotomayor (2015)
|
|
Tabebuia rosea
|
592
|
879
|
1,48
|
Sotomayor (2016)
|
|
Hevea brasiliensis
|
605
|
1008
|
1,67
|
Nadir et al. (2014)
|
|
Taxus baccata
|
650
|
1650
|
2,54
|
Keunecke et al. (2007)
|
|
Fagus sylvatica
|
689
|
1010
|
1,47
|
Ozyhar et al. (2013)
|
|
Andira inermis
|
716
|
1084
|
1,51
|
Sotomayor (2018a)
|
|
Lysiloma acapulcensis
|
716
|
1328
|
1,85
|
Sotomayor (2016)
|
|
Fagus crenata
|
740
|
637
|
0,86
|
Naruse (2003)
|
|
Psidium sartorianum
|
789
|
1067
|
1,35
|
Sotomayor (2018a)
|
|
Juglans pyriformis
|
810
|
1369
|
1,69
|
Sotomayor (2018a)
|
|
Caesalpinia platyloba
|
825
|
1511
|
1,83
|
Sotomayor (2018a)
|
|
Albizia plurijuga
|
844
|
1792
|
2,12
|
Sotomayor (2018a)
|
|
Quercus scytophylla
|
933
|
1294
|
1,39
|
Sotomayor (2015)
|
|
Acosmium panamense
|
1005
|
1622
|
1,61
|
Sotomayor (2018a)
|
|
Tabebuia chrysantha
|
1096
|
2320
|
2,12
|
Sotomayor (2018a)
|
|
Cordia elaeagnoides
|
1135
|
2157
|
1,90
|
Sotomayor (2016)
|
|
ρCH = Densidad; GLT
= Módulo de rigidez: *Itor = Índice material (m2 s-2
× 10-6).
|
Entre los métodos que utilizan se pueden mencionar: las
frecuencias de vibraciones torsionales en placas de madera posicionadas como
vigas en voladizo (Wang et al., 2018); los ensayos de compresión estática
(Hernández & Sotomayor, 2014); la utilización de vibraciones transversales
(Sotomayor, 2018a); ensayos de compresión estática (Anshari et al., 2011); el
estudio de placas de madera con frecuencias derivadas de vibraciones
torsionales (Roohnia & Kohantorabi, 2015; Sotomayor, 2016); pruebas de
flexión estática con cuatro puntos, complementa-das con el método del elemento
finito (Naruse, 2003); uso de ultrasonido (Ozyhar et al., 2013); pruebas de
cortante estática (Nadir et al., 2014); valores de módulos GLT
estimados a partir de modelos teóricos (Sotomayor, 2015); pruebas de cortante
estática (Komán & Feher, 2017); utilización de ultrasonido (Keunecke et
al., 2007; Kránitz et al., 2014); empleo de placas de madera deformadas en
torsión estática (Yoshihara, 2012); combinación de pruebas de flexión estática
y dinámica con el método del elemento finito (Olsson & Källsner, 2013);
ondas de esfuerzo (Cha, 2015); y el estudio de placas de madera con vibraciones
torsionales en el plano tangencial-longitudinal (Sotomayor & Villaseñor,
2016).
El módulo de rigidez de la madera
varía igualmente por la heterogeneidad estructural propia de cada especie, el
tamaño de las probetas ensayadas y según sus direcciones de anisotropía (Wang
et al., 2023). De tal forma, que los métodos dinámicos no destructivos se
prospectan como técnicas apropia-das para determinar estas constantes
materiales en probetas de pequeñas dimensiones. Valores para el módulo de
rigidez correspondientes a los planos longitudinal-radial y/o
radial-longitudinal de la madera y determinados con diferentes técnicas están
reportados por Krüger & Wagenführ (2020) para
Fagus sylvatica (973 MN m-2 < GLR <
1289 MN m-2) y Picea abies (973 MN m-2 <
GRL < 1289 MN m-2).
En el mismo contexto, Sylvayanti et al.
(2023) informan sobre datos del módulo de rigidez determinado en pruebas
estáticas y correspon-diente al plano longitudinal-tangencial de Agathis
sp.: 207 MN m-2; Swietenia sp.: 266 MN m-2; Shorea
sp.: 262 MN m-2; y Pinus spp.: 242 973 MN m-2. Debido
a las propiedades de anisotropía en las características elásticas de la madera (Zhang
et al., 2022) y a los diferentes tipos de pruebas empleadas para su
determinación, los datos citados no son comparables con los referidos en la
Tabla 1.
La variabilidad en las magnitudes de la densidad y del
módulo de rigidez amplía la prospectiva para diseñar productos a base de
madera. Así, la selección de una especie empleando índices materiales como
criterio de preferencia es conveniente para especificar los valores mínimos
admisibles para el análisis estructural y puede utilizarse para reglamentos de
edificación con madera (Sotomayor, 2018b). En este contexto, el índice material
de una pieza de madera que trabaja en torsión es el parámetro que relaciona su
módulo de rigidez con su densidad. Además, es un indicador sobre la calidad de
la madera para usos constructivos. Un alto índice material de una madera
sugiere una mejor resistencia en relación con la densidad, y una buena
apreciación como material de ingeniería (Ashby, 2011).
En los trabajos citados, se registra variabilidad en
los resultados según la especie en estudio, así como la técnica empleada para
la determinación de los módulos de rigidez. Se observa igualmente que sus
magnitudes aumentan proporcionalmente a la densidad de las maderas. Así, surge
la pregunta de investigación si las magnitudes del módulo de rigidez
determinado en probetas recortadas de piezas de madera comercial son similares
a los datos reportados en la bibliografía calculados con probetas ex profeso
para fines de investigación. Esta inquietud refiere a los códigos de
construcción con madera que establecen protocolos para la determinación de
parámetros de ingeniería y especifican ajustes para el cálculo y diseño de
estructuras de madera (American Wood Council, 2015; Canadian Wood Council,
2017).
Los factores que se toman en cuenta para satisfacer los
criterios de diseño son, entre otros: la duración de la carga, la variabilidad
natural de la madera, las condiciones especiales de servicio, la geometría de
la pieza y el tipo de ensayo del cual proviene el esfuerzo permisible
calculado; los defectos, magnitud, frecuencia y combinación de irregularidades
tales como nudos, desviación del grano, rajaduras, ondulación y degradación biológica;
y el factor de corrección para el contenido de humedad en servicio, dependiendo
de la exposición a la intemperie o a fuentes cercanas de humedad (American
Institute of Timber Construction, 2012).
Las especies comerciales P. pseudostrobus,
T. rosea y Q. scytophylla son endémicas de México y
Centro América y presentan potencial para la fabricación de productos de alto
valor agregado. Información sobre sus características físicas y mecánicas está
reportada por Sotomayor (2015). Sin embargo, no existe información sobre sus
módulos de rigidez e índices de materiales.
Como hipótesis de trabajo, la investigación plantea que
las magnitudes de los módulos de rigidez de las maderas comerciales
P. pseudostrobus, T. rosea y Q. scytophylla son del
mismo orden que las reportadas en la bibliografía, pero diferentes entre
especies. Para verificar esta hipótesis, el objetivo de la investigación fue
determinar sus módulos de rigidez realizando pruebas de torsión dinámica.
La verificación de la hipótesis pretende propor-cionar
certeza para el usuario de la madera de que los datos obtenidos en laboratorio,
con los ajustes requeridos por la normatividad, son confiables en el cálculo y
diseño de productos de madera. Para complementar el estudio, se calculan los
índices materiales para datos reportados en la bibliografía y se comparan con
los índices materiales de P. pseudostrobus, T. rosea y Q.
scytophylla, calculados en esta investigación.
Se adquirieron
lotes de madera aserrada y estufada en un establecimiento comercial en la
ciudad de Morelia, México y se prepararon probetas de P. pseudostrobus, T.
rosea y Q. scytophylla. No se mesclaron muestras de diferentes
especies de un solo género. El taxón botánico se identificó en la Facultad de
Ingeniería en Tecnología de la Madera, de la Universidad Michoacana de San
Nicolás de Hidalgo, en Morelia, México. La madera no contenía defectos de crecimiento
tales como nudos o desviación de la fibra. Las dimensiones de las probetas
fueron 0,02 m de espesor por 0,15 m de ancho y 0,15 m de largo, alineadas de
tal forma que las dimensiones correspondieron a las direcciones radial,
tangencial y longitudinal del plano leñoso. Las probetas se almacenaron en una
cámara de acondicionamiento con temperatura de 20°C (± 2°C) y una humedad
relativa del aire de 65% (±5%) hasta que la madera alcanzó su contenido de
humedad en equilibrio promedio de 8%.
El contenido de
humedad (CH) de las probetas se determinó con la relación peso al momento del
ensayo y el peso de la probeta en estado seco, adaptando la norma ISO
13061-1:2014 (International Organization for Standardization, 2014a). La
densidad de la madera (ρCH), correspondiente a un contenido de
humedad, se calculó con el cociente del peso de la madera y el volumen de esta
al momento del ensayo, adaptando la norma ISO 13061-2:2014 (International
Organization for Standardization, 2014b).
Las pruebas de
vibración en torsión adaptaron el protocolo recomendado por la norma ASTM
C1259-14 (American Society for Testing and Materials, 2015a) y siguen el
procedimiento descrito en Sotomayor (2016). La probeta se posicionó sobre
soportes aislantes en medio del ancho (b) y del largo (l) de las probetas,
formando una cruz (Figura 1). La probeta fue solicitada en la dirección radial,
perpendicularmente a la dirección longitudinal en el plano tangencial-radial,
lo que ocasionó vibraciones en torsión en el plano correspondiente a las direcciones
longitudinal y tangencial, de tal forma, que el módulo de rigidez calculado
corresponde al plano longitudinal-tangencial.
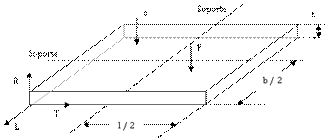
Figura 1. Diagrama de
las pruebas de vibraciones en torsión. P: posición para aplicar el impacto; s:
posición para medir la frecuencia natural; R: dirección radial (t: espesor); T:
dirección tangencial (l: largo); L: dirección longitudinal (b: ancho). Adaptado
de la norma ASTM C1259-15.
De acuerdo con
la norma ASTM E1876-15 (American Society for Testing and Materials, 2015b) en
cada una de las 35 probetas de cada especie se aplicó un impacto empleando una
esfera de acero de 0,005 m de diámetro, adherida a un cabo elástico de 0,01 m
de longitud y de 0,002 m de espesor por 0,007 m de ancho. El impacto fue
aplicado en el punto P de la superficie de la probeta, localizado en la
intersección de 0,25 del ancho (b) y a 0,25 del largo (l) de cada espécimen
(Figura 1). Empleando un aparato Grindosonic® modelo MKS, se registró el
movimiento de la probeta en el punto (s), en una posición simétrica respecto al
punto de impacto. La lectura del sensor piezo-eléctrico de movimiento se
transforma en una señal eléctrica, la cual, a su vez, es convertida en la
frecuencia natural (f) del sistema, con una precisión de lectura de 0,005%. El
módulo de rigidez es rubricado con el subíndice LT para identificarlo como
derivado de pruebas de torsión en el plano longitudinal-tangencial de la
madera.
El módulo de
rigidez de la madera por vibraciones en torsión se calculó con la fórmula (1)
(American Society for Testing and Materials, 2015b):
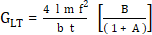 (1)
(1)
Con:
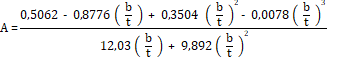
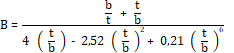
Donde:
GLT =
Módulo de rigidez (N m-2)
f = Frecuencia
natural (Hz)
m = masa de la
probeta (g)
l = Largo de la
probeta (Dirección tangencial) (m)
t = Espesor de
la probeta (Dirección radial) (m)
b = Ancho de la
probeta (Dirección longitudinal) (m)
A y B = Factores
de ajuste geométrico
El índice
material se calculó con la fórmula (2) (Ashby, 2011):
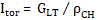 (2)
(2)
Donde:
Itor
= Índice material (m2 s-2)
GLT =
Módulo de rigidez (MN m-2)
ρCH
= Densidad (kg m-3)
Diseño
experimental
La estrategia experimental
se orientó hacia la comparación de resultados entre especies. Se observaron 35
probetas por cada especie. Las variables de respuesta fueron los valores de la
densidad (ρCH) y de la frecuencia (f); el módulo de rigidez (GLT),
calculado con la fórmula (1) y el índice material (Itor), calculado
con la fórmula (2), son variables derivadas. De tal forma, se formaron nueve
muestras independientes (tres variables × tres especies). Para cada muestra se
calcularon su media (μ), su desviación estándar (σ) y su coeficiente
de variación (CV = σ/μ). Se calcularon las correlaciones lineales (y
= ax + b) y los coeficientes de determinación (R2) de los módulos de
rigidez en función de la densidad y de la frecuencia. Igualmente, se calculó la
correlación lineal entre el índice material y la densidad y se complementaron
con correlaciones empleando datos de la bibliografía (Tabla 1).
Los cálculos
estadísticos se efectuaron con el programa Stagraphics Centurion XV. Las
ponderaciones para calificar la intensidad de las correlaciones fueron los
valores del coeficiente de determinación: correlación muy alta: 1 ≥ R2
≥ 0,9; correlación alta: 0,9 > R2 ≥ 0,7; correlación
media: 0,7 > R2 ≥ 0,4; correlación baja: 0,4 > R2
≥ 0,2; y correlación nula: R2 < 0,2.
Para validar en
número de probetas medidas en cada una de las tres especies se calculó el
tamaño de la muestra con la fórmula (3) (Gutiérrez & De la Vara, 2009):
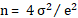 (3)
(3)
Donde:
n = Tamaño de la
muestra
σ =
Desviación estándar
e = Error de
estimación aceptable (0,05).
Densidades
Las magnitudes de las
densidades de las maderas de P. pseudostrobus, T. rosea y Q.
scytophylla se ubican al interior del intervalo reportadas en la
bibliografía (Tabla 1). El coeficiente de variación de P. pseudostrobus
es 125% más grande respecto al de T. rosea y Q. scytophylla
(Tabla 2). Asimismo, los coeficientes de variación se sitúan al interior del
rango para las especies estudiadas en esta investigación (Sotomayor, 2015).
Tabla 2
Resultados de las pruebas
de vibraciones en torsión
|
|
ρCH
|
f
|
GTL
|
Itor
|
|
|
(kg m-3)
|
(Hz)
|
(MN m-2)
|
(m2
s-2 × 10-6)
|
|
|
P.
pseudostrobus
|
|
μ
|
587
|
1088
|
906
|
1,54
|
|
σ
|
48
|
77
|
146
|
0,22
|
|
CV
|
(8,2)
|
(7,1)
|
(16,2)
|
(14,2)
|
|
|
T. rosea
|
|
μ
|
565
|
1115
|
915
|
1,62
|
|
σ
|
21
|
68
|
121
|
0,21
|
|
CV
|
(3,7)
|
(6,1)
|
(13,2)
|
(13,1)
|
|
|
Q. scytophylla
|
|
μ
|
735
|
1059
|
1068
|
1,45
|
|
σ
|
25
|
30
|
71
|
0,09
|
|
CV
|
(3,4)
|
(2,8)
|
(6,6)
|
(6,2)
|
ρCH =
densidad; f = Frecuencia; GLT = Módulo de rigidez; Itor =
Índice material; μ = Media; σ = desviación estándar; CV = Coeficiente
de variación en porciento y entre paréntesis.
Frecuencias
Las frecuencias medidas de
las tres maderas son similares entre sí (Tabla 2). Sin embargo, el coeficiente
de variación de Q. scytophylla es 50% menor comparativamente con los
coeficientes de P. pseudostrobus y T. rosea. Estos valores son
razonables en mediciones de frecuencias en torsión en maderas (Sotomayor &
Villaseñor, 2016).
Módulos de rigidez
Los módulos de rigidez
calculados con la fórmula (1) son similares a los reportados en la bibliografía
para maderas con densidades equivalentes (Tabla 1). El coeficiente de variación
para P. pseudostrobus es 23% mayor que el de T. rosea y 146%
mayor que el de Q. scytophylla, valores aceptables en caracterización
mecánica de la madera (Sotomayor, 2018a).
Índices materiales
Para las tres especies
estudiadas en esta investigación, sus índices materiales calculados con la
fórmula (2) y listados en la Tabla 2 son comparables a los calculados a partir
de datos de la bibliografía para especies con densidad similar (Tabla 1). El índice
material de T. rosea es 5,2% mayor respecto al de P. pseudostrobus,
una especie considerada en esta investigación como referencia por su uso
extendido en la industria de la madera. En cambio, el de Q. scytophylla
es 5,8% menor.
Tamaño de la muestra
Para las tres maderas el
número de probetas observadas por especies fue de 35 unidades, cantidad mayor
al tamaño de muestra necesario para satisfacer el requisito de una muestra
representativa calculado con la fórmula (3). Así, el tamaño de muestra en función
del error aceptable para la densidad (Figura 2) y la frecuencia (Figura 3)
convergen hacia los valores presentados en la Tabla 3.
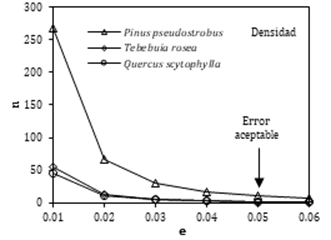
Figura 2. Cálculo del
tamaño de la muestra (n) para la densidad (ρCH) en función del
error aceptable (e).
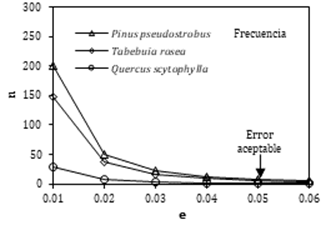
Figura 3. Cálculo del
tamaño de la muestra (n) para la frecuencia (f) en función del error aceptable
(e).
Tabla 3
Resultados del cálculo del
tamaño de la muestra
|
Especies
|
e
|
ρCH
|
f
|
|
-
|
n
|
n
|
|
P. pseudostrobus
|
0,05
|
11
|
8
|
|
T. rosea
|
0,05
|
2
|
6
|
|
Q. scytophylla
|
0,05
|
2
|
1
|
e = Error de estimación
aceptable; ρCH = densidad; f = Frecuencia; n = Número de
muestra.
La frecuencia natural en
vibraciones por torsión aumenta cuando la densidad de la madera incrementa. La
frecuencia natural es un predictor del módulo de rigidez con una correlación de
GLT = 3,41 ρCH - 7,288 y R2 = 0,81. Los
valores del GLT de las tres especies mexicanas son similares a los
módulos de rigidez para el plano longitudinal-tangencial determinados por los
autores Naruse (2003), Keunecke et al. (2007), Yoshihara (2012), Ozyhar et al.
(2013), Kránitz et al. (2014), Nadir et al. (2014) y Sotomayor (2015), para
maderas con densidades y contenidos de humedad similares a los determinados en
el presente estudio.
El estudio demuestra que
para las especies de madera de P. pseudostrobus y T. rosea la
frecuencia es un buen predictor del módulo de rigidez. Sus correlaciones
califican como altas. Sin embargo, para la madera de Q. scytophylla el
coeficiente de determinación del modelo de predicción lineal califica como una
correlación media (Figura 4). Este estudio revela una observación interesante
sobre la divergencia en la correlación entre el módulo de rigidez y la
densidad. Al interior de una misma especie, la variabilidad natural de la
madera ocasiona que el módulo de rigidez no correlacione bien con la densidad.
No obstante, los valores promedio se sitúan en la tendencia lineal que resulta
de la correlación calculada con los valores reportados en la bibliografía.
Así, la investigación
demuestra que la densidad y los módulos de rigidez de P. pseudostrobus, T.
rosea y Q. scytophylla son diferentes entre especies, pero de la
misma magnitud que los correspondientes a otras especies de densidad similar.
La validez de este corolario se restringe al estudio de una muestra de madera,
representativa de las tres especies, y a los resultados obtenidos de pruebas
dinámicas de torsión.
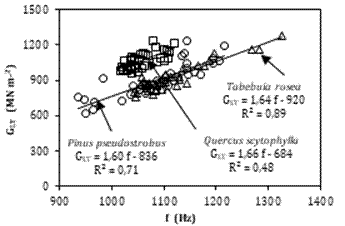
Figura 4. Correlaciones
entre el módulo de rigidez (GLT) y la frecuencia (f).
Los valores determinados
del módulo de rigidez presentan variabilidad en dos aspectos. Por una parte, al
interior de una misma especie, las mediciones correlacionadas en función de su
densidad muestran una amplia dispersión explicada por coeficientes de regresión
nulos (Figura 5). Para T. rosea el coeficiente de determinación indica
una relación inexistente. Este parámetro mejora para Q. scytophylla y P.
pseudostrobus. Por otra parte, se observa que los valores promedio de esta
investigación se posicionan cerca de la correlación GLT = f(ρCH)
calculada con los datos de la bibliografía (Figura 6), la cual califica como
alta de acuerdo a los criterios propuestos en el diseño experimental. Además,
la correlación de los tres valores promedio de P. pseudostrobus, T.
rosea y Q. scytophylla, resulta con un coeficiente de determinación
29% mayor al calculado para las 26 especies detalladas en la Tabla 1.
Estos resultados coinciden
con los reportados por Sotomayor (2016) quien, utilizando un procedi-miento
experimental similar al de la presente investigación, reporta que el módulo de
rigidez de la madera aumenta proporcionalmente a su densidad para siete
especies tropicales. Igual-mente, Sotomayor (2018) confirma este para-digma,
pero aplicando vibraciones transversales en 22 maderas. Sin embargo, Olsson&
Källsner (2013) y Cavalli et al. (2017) reportan que, para el caso de piezas de
madera aserrada con dimensiones de empleo, tales como tablas, tablones y vigas,
los coeficientes de determinación entre módulo de rigidez y densidad son de R2
= 0,22.
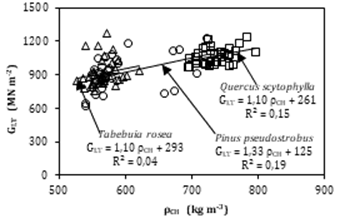
Figura 5. Correlaciones
entre el módulo de rigidez (GLT) y la densidad (ρCH).
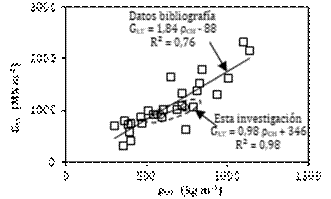
Figura 6. Correlaciones
entre los módulos de rigidez (GLT) y las densidades (ρCH)
con datos de la bibliografía (Tabla 1) y resultados de esta investigación.
Los resultados de
laboratorio ensayando probetas de pequeñas dimensiones y libres de defectos,
como es el caso de la presente investigación, no son necesariamente similares a
los resultados obtenidos con piezas de grandes dimensiones que tienen nudos y/o
anomalías de crecimiento. De aquí se induce que para obtener datos útiles en
cálculo ingenieril es recomendable experimentar con piezas de dimensiones
reales de empleo. Los valores reportados en esta investigación pueden ser
útiles si estas especies de maderas se utilizan con fines estructurales. Sin
embargo, las magnitudes son solo indicativas y no representan el promedio de
las especies debido al número limitado de muestras analizadas. Se recomienda
aplicar los protocolos de cálculo estructural requeridos por la normatividad en
ingeniería de la madera.
El índice material de la
madera es la combinación de las propiedades fisicoquímicas, las cuales
caracterizan su rendimiento para una aplicación específica (Ashby, 2011). Por
ejemplo, un buen diseño de estructuras de madera puede contribuir a mejorar el
ambiente sonoro en construcciones, gracias a las propiedades acústicas del
material. Entre otros indicadores de calidad de los materiales de construcción,
el índice material que relaciona su módulo de rigidez con su densidad es un
indicador de la calidad de la madera para usos específicos. El índice material
de P. pseudostrobus, T. rosea y Q. scytophylla es
diferente en cada especie (Tabla 2, Figura 7).
Las especies que muestran
altos valores del índice material poseen un potencial de calidad para su empleo
en la industria de la construcción y en aplicaciones donde las propiedades de
resistencia en solicitaciones y deformaciones fuera de plano son importantes.
Las especies estudiadas se
posicionan al interior de la nube de dispersión para maderas reportadas en la
bibliografía (Tabla 1 y Figura 7) y son menores comparativamente con otros
materiales de uso contractivo como los mostrados en la Figura 8. Es importante
hacer notar que estos índices de materiales constructivos son calculados
relacionando el módulo de elasticidad en lugar del módulo de rigidez utilizado
en la presente investigación. La Figura 8 se presenta sólo para dar una idea
del orden de las magnitudes de la madera y otros materiales comerciales.
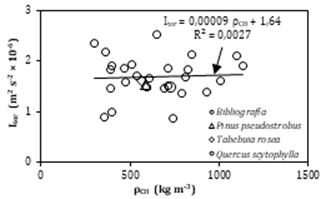
Figura 7. Dispersión del
índice material (Itor) en función de la densidad (ρCH).

Figura 8. Índices
materiales (Itor) de P. pseudostrobus, T. rosea y Q.
scytophylla (esta investigación) y de materiales de construcción (Ashby,
2011).
Los índices materiales
determinados en probetas de madera comercial son comparables con datos de
especies de densidades parecidas y determinados con experimentos similares a
los de la presente investigación (Sotomayor, 2015; Sotomayor 2016; Tabla 1).
Respecto a P. pseudostrobus y Q. scytophylla los
índices materiales son similares a los de P. pseudostrobus y Q.
scytophylla. En relación con Tabebuia rosea, el índice de T.
rosea es 29% mayor.
Los
resultados muestran que las magnitudes de los módulos de rigidez de maderas de P.
pseudostrobus, T. rosea y Q. scytophylla son del mismo orden
que las reportadas en la bibliografía, pero diferentes entre especies. La
estrategia experimental se orientó hacia el análisis de resultados especie por
especie, con el objetivo de caracterizar las maderas de P. pseudostrobus,
T. rosea y Q. scytophylla con un enfoque empírico de caso por
caso de una especie en particular. El procedimiento está referido a las
condiciones de ensayo: la densidad y el contenido de humedad de la madera y con
datos derivados de un tamaño de muestra estadísticamente repre-sentativa.
Los
resultados permiten proponer la utilización de las especies
caracterizadas en elementos estructu-rales de diferentes formas, secciones y
longitudes. Sus posibles usos son en las industrias de la Arquitectura y de la
construcción, así como para la elaboración de muebles y utensilios de madera.
La
investigación estuvo patrocinada por la Coor-dinación de la Investigación
Científica de la Universidad Michoacana de San Nicolás de Hidalgo, Morelia,
Michoacán, México.
REFERENCIAS
BIBLIOGRÁFICAS
American Institute of Timber Construction. (2012).
Timber Construction Manual. USA, Englewood: American Institute of Timber
Construction.
American Society for Testing and Materials. (2015a).
ASTM C1259-15. Standard test method for dynamic Young’s modulus, shear
modulus, and Poisson’s ratio for advanced ceramics by impulse excitation of vibration.
USA, West Conshohocken: American Society for Testing and Materials.
American Society for Testing and Materials. (2015b).
ASTM E1876-15. Standard test method for dynamic Young’s modulus, shear
modulus, and Poisson’s ratio by impulse excitation of vibration. USA, West
Conshohocken: American Society for Testing and Materials.
American Wood Council. (2015). National Design
Specifications (NDS) for Wood Construction with
Commentary. USA, Lessbourg: American Wood
Council.
Anshari, B., Guan, Z. W., Kitamori,
A., Jung, K., Hassel, I., & Komatsu, K. (2011). Mechanical and
moisture-dependent swelling properties of compressed Japanese cedar. Construction
and Building Materials, 25(4), 1718-1725. doi:
https://doi.org/10.1016/j.conbuildmat.2010.11.095
Ashby, M. F. (2011). Materials
selection in mechanical design. England, London: Butterworth-Heinemann.
Brandner, R., Tomasi, R., Moosbrugger,
T., Serrano, E., & Dietsch, P. Editors. (2018). Properties, Testing and
Design of Cross Laminated Timber: A state-of-the art report by Cost action
FP1402/WG2. Germany, Aachen: Shaker Verlag. doi: https://doi.org/10.2370/9783844061437
Canadian Wood Council. (2017). Wood
Design Manual 2017. Vol. 1 & 2. Canada, Ottawa: Canadian Wood Council.
Cavalli, A., Cibecchini, D., Goli, G.,
& Togni, M, (2017). Shear modulus of old timber. iForest,
10, 446-450. doi:
https://doi.org/10.3832/ifor1787-009
Cha, J. K. (2015). Determination of
true modulus of elasticity and modulus of rigidity for domestic woods with
different slenderness ratios using nondestructive tests. Journal of the
Korean Wood Science and Technology, 43(1), 36-42. doi:
https://doi.org/10.5658/WOOD.2015.43.1.36
Chauhan, S., & Sethy, A. (2016).
Differences in dynamic modulus of elasticity determined by three vibration
methods and their relationship with static modulus of elasticity. Maderas.
Ciencia y tecnología, 18(2), 373-382. doi: http://dx.doi.org/10.4067/S0718-221X2016005000034
Echenique, C. S., Banda, B. I., &
Hernández, J. R. (2015). Physical and Mechanical Properties of the Wood Used in
Indigenous Housing of the Tuchín Township, Department of Cordoba. Colombia.
INGE CUC, 11(1), 99-108. doi:
https://doi.org/10.17981/ingecuc.11.1.2015.10
Gutiérrez, H., & De la Vara, R. (2009).
Análisis y diseño de experimentos. México, México: McGraw-Hill.
Hernández, S. A., & Sotomayor, J.
R. (2014). Comportamiento elástico de la madera de Acer rubrum y
de Abies balsamea. Madera y Bosques, 20(3),
113-123. doi: https://doi.org/10.21829/myb.2014.203156
International Organization for
Standardization. (2014a). ISO 13061-1:2014. Physical and mechanical
properties of wood -- Test methods for small clear wood specimens -- Part 1:
Determination of moisture content for physical and mechanical tests. Switzerland,
Geneva: International Organization for Standardization.
International Organization for
Standardization. (2014b). ISO 13061-2:2014. Physical and mechanical
properties of wood -- Test methods for small clear wood specimens -- Part 2:
Determination of density for physical and mechanical tests. Switzerland, Geneva:
International Organization for Standardization.
Jacob, M., Harrington, J., &
Robinson, B. (2018). The Structural Use of Timber Handbook for Eurocode 5:
Part 1-1. Ireland, Dublin: COFORD, Department of Agriculture, Food and the
Marine.
Jaskowska-Lemanska, J., &
Przesmycka, E. (2020). Semi-Destructive and Non-Destructive Tests of Timber
Structure of Various Moisture Contents. Materials, 14, 96-118. doi:
https://doi.org/10.3390/ma14010096
Keunecke, D., Sonderegger, W.,
Pereteanu, K., Lüthi, T., & Niemz, P. (2007). Determination of Young’s and
shear moduli of common yew and Norway spruce by means of ultrasonic waves. Wood
Science and Technology, 41(4), 309-327. doi:
https://doi.org/10.1007/s00226-006-0107-4
Komán, S., & Feher, S. (2017).
Physical and mechanical properties of Paulownia tomentosa wood planted
in Hungaria. Wood Research, 62(2), 335-340.
Kránitz, K., Deublein, M., &
Niemz, P. (2014). Determination of dynamic elastic moduli and shear moduli of
aged wood by means of ultrasonic devices. Materials and Structures, 47(6),
925-936. doi: https://doi.org/10.1617/s11527-013-0103-8
Krüger, R., & Wagenführ, A.
(2020). Comparison of methods for determining shera modulus of wood. European
Journal of Wood and Wood Products, 78, 1087-1094. doi: https://doi.org/10.1007/s00107-020-01565-2
Llana, D. F., Íñiguez-González, G.,
Díez, M. R., & Arriaga, F. (2020). Nondestructive
testing used on timber in Spain: A literature review. Maderas. Ciencia
y tecnología, 22(2), 133-156. doi: http://dx.doi.org/10.4067/S0718-221X2020005000201
Malesza, J. (2015). Possible defects
in wood, wood parameters variability and some of its influence on quality of
building structure. Engineering Structures and Technologies, 7(2),
67-80. doi: https://doi.org/10.3846/2029882X.2016.1123895
Nadir, Y., Nagarajan, P., &
Midhun, A. J. (2014). Measuring elastic constants of Hevea brasiliensis
using compression and Iosipescu shear test. European Journal of Wood and
Wood Products, 72(6), 749-758. doi: https://doi.org/10.1007/s00107-014-0842-4
Naruse, K. (2003). Estimation of shear
moduli of wood by quasi-simple shear tests. Journal of Wood Science, 49(6),
479-484. doi: https://doi.org/10.1007/s10086-003-0515-0
Olsson, A., & Källsner, B. (2013).
Shear modulus of structural timber evaluated by means of dynamic excitation and
FE analysis. Materials and Structures, 48(4), 977-985. doi:
https://doi.org/10.1617/s11527-013-0208-0
Ozyhar, T., Hering, S., Sanabria, S.
J., & Niemz, P. (2013). Determining moisture-dependent elastic
characteristics of beech wood by means of ultrasonic waves. Wood Science and
Technology, 47(2), 329-341. doi: https://doi.org/10.1007/s00226-012-0499-2
Rocco, F. A., Christoforo, A. L.,
Varanda, L. D., Chahud, E., Almeida, V., & Nunes, L. A. M. (2017). Shear
and Longitudinal Modulus of Elasticity in Wood: Relations Based on Static
Bending Tests. Acta Scientiarum. Technology, 39(4), 433-437. doi:
https://doi.org/10.4025/actascitechnol.v39i4.30512
Roohnia, M., & Kohantorabi, M. (2015).
Dynamic methods to evaluate the shear modulus of Wood. BioResources, 10(3),
4867-4876. doi:
https://doi.org/10.15376/biores.10.3.4867-4876
Sotomayor, J. R. (2015). Banco
FITECMA de características físico-mecánicas de maderas mexicanas. México, Morelia:
Universidad Michoacana de San Nicolás de Hidalgo. doi: https://doi.org/10.13140/RG.2.1.3497.4884
Sotomayor, J. R. (2016). Módulos de
rigidez dinámicos de siete maderas mexicanas determinados por vibraciones en
torsión. Revista Chapingo Serie Ciencias Forestales y del Ambiente, 22(2),
125-134. doi:
https://doi.org/10.5154/r.rchscfa.2015.03.008
Sotomayor, J. R. (2018a).
Características dinámicas de 22 maderas determinadas por el método de
vibraciones transversales. Revista Mexicana de Ciencias Forestales, 9(48),
1-23. doi:
https://doi.org/https://doi.org/10.29298/rmcf.v8i48.150
Sotomayor, J. R. (2018b). Índices
materiales en flexión estática de maderas mexicanas con potencial para uso en
la construcción. Ingeniería Mecánica Tecnología y Desarrollo, 6(2),
45-52.
Sotomayor, J. R., & Villaseñor, J.
M. (2016). Módulo de rigidez y módulo dinámico de la madera de Acer saccharum
Marshall y Thuja plicata L. Revista Forestal Mesoamericana
Kurú, 13(33), 20-28. doi: https://doi.org/10.18845/rfmk.v13i33.2574
Sylvayanti, S. P., Nugroho, N., &
Bahtiar, E. T. (2023). Bamboo Scrimber’s Physical and
Mechanical Properties in Comparison to Four Structural Timber Species. Forest,
14, 146. doi: https://doi.org/10.3390/f14010146
Wang, Z., Xie, W., Wang, Z., &
Cao, Y. (2018). Strain method for synchronous dynamic measurement of elastic,
shear modulus and Poisson’s ratio of wood and wood composites. Construction
and Building Materials, 182, 608-619. doi: https://doi.org/10.1016/j.conbuildmat.2018.06.139
Wang, Z., Zhang, D., Wang, Z., Liang,
X., Yang, X., & Wang, J. (2023). Research Progress on Dynamic Testing
Methods of Wood Shear Modulus: A Review. BioResources, 18(1), 2262-2270.
Yoshihara, H. (2012).
Shear modulus and shear strength evaluation of solid wood by a modified ISO
15310 square-plate twist method. Drvna Industrija, 63(1), 51-55. doi:
https://doi.org/10.5552/drind.2012.1125
Zhang, L., Li, Q., Liu, W., He, Q., Liu, Y., &
Guo, K. (2022). Evaluation of the Shear Performance of Douglas-FirWood at
Elevated Temperatures. materials, 15, 8386. https://doi.org/10.3390/ma15238386
![]() https://orcid.org/0000-0002-1527-8801 I. Macedo
Alquecira:
https://orcid.org/0000-0002-1527-8801 I. Macedo
Alquecira: ![]() https://orcid.org/0000-0002-6432-6574
https://orcid.org/0000-0002-6432-6574![]() https://orcid.org/0000-0002-3662-3272
https://orcid.org/0000-0002-3662-3272