INTRODUCCIÓN
Desempeño de métodos deterministas en la estimación del tiempo de concentración en la cuenca alta del Jequetepeque, Perú
Performance of deterministic methods in estimating the concentration time in the upper basin of Jequetepeque, Peru
Jairo Isaí Alvarez Villanueva1; José Francisco Huamán Vidaurre1
*Autor corresponsal: jialvarezv@unc.edu.pe (J. I. Alvarez Villanueva).
ID ORCID de los autores:
J. I. Alvarez Villanueva: https://orcid.org/0000-0001-8777-3943
J. F. Huamán Vidaurre: https://orcid.org/0000-0002-4896-0479
RESUMEN
El objetivo fue determinar el desempeño de métodos deterministas para estimar el tiempo de concentración (tc) para la cuenca alta del Jequetepeque, Perú. Se utilizó 32 métodos deterministas, relacionados con parámetros morfológicos de la cuenca alta, tales como: área de cuenca, longitud de cauce principal, pendiente media del cauce principal, coeficiente de escorrentía, número de curva y distancia del punto emisor al centro de gravedad. Estos parámetros, se obtuvieron a partir de modelos digitales de elevación de 12,5 m de precisión. Los resultados de tc fueron obtenidos según la metodología de Martínez (2005). De los modelos deterministas aplicados a la cuenca de estudio, el 34% lograron aproximarse al rango del tiempo de concentración (6 a 12 horas). El tiempo de concentración calculado para la cuenca en estudio es 8,61 horas. Este tiempo es fundamental para estimar el caudal máximo y aplicarlos en diseño de estructuras hidráulicas, sistemas de drenaje eficientes y riesgo de inundaciones, entre otros.
Palabras clave: tiempo de concentración, cuenca del Jequetepeque, métodos deterministas, gota de agua.
ABSTRACT
The objective was to determine the performance of deterministic methods to estimate the time of concentration (tc) for the upper Jequetepeque basin, Peru. These 32 deterministic methods were used, it related to morphological parameters of the upper basin, such as basin area, length of main riverbed, average slope of the main riverbed, overflow coefficient, number of curve and distance from the emitting point to the center of gravity. These parameters were obtained from digital elevation models of 12.5 m precision. The CT results were obtained according to the methodology of Martinez (2005). From the deterministic models applied to the study basin, 34% managed to approach the concentration time range (6 to 12 hours). The concentration time calculated for the basin under study is 8.61 hours. This time is essential for estimating peak flow and applying it in the design of hydraulic structures, efficient drainage systems, flood risk management, and more.
Keywords: concentration time, Jequetepeque watershed, deterministic methods. water droplet.
Recibido: 25-08-2024.
Aceptado: 10-11-2024.
El concepto de tiempo de concentración (Tc) como respuesta de una cuenca frente a un evento de lluvia, tiene una antigüedad de más de 150 años, desde la creación del método racional. Hasta la fecha, el tiempo de concentración es estimado mediante las características de la cuenca, este tiempo es el insumo más importante para el hidrograma unitario (Beven, 2020). El tiempo de concentración es un parámetro hidrológico propio de cada cuenca hidrológica (Martínez Alvarez, 2006). Este parámetro, es el tiempo más importante en que la lluvia genera escorrentía y es utilizado para estimar el caudal máximo y riesgos de inundación (Sultan et al., 2022; Alamri et al., 2023). La definición más común sobre el tiempo de concentración es el tiempo que una gota de lluvia escurre superficialmente desde un punto o lugar más alejado hidráulicamente de una unidad hidrográfica al punto de descarga o punto emisor. Es el tiempo en el cual, toda la unidad hidrográfica aporta o contribuye al flujo en el punto emisor, cuando la lluvia es uniforme y cubre toda la cuenca (Yoo et al., (2019; Hotchkiss & McCallum, 1995). Más del 75% de errores para estimar el caudal máximo de cuenca, se deben a la mala determinación del tiempo de concentración. Trayendo problemas en el dimensionamiento de infraestructura y socioeconómicas (Bondelid et al., 1982; Gericke & Smithers, 2014). Existe la necesidad de representar el tiempo de respuesta de una cuenca frente a una tormenta, para fines de diseño hidrológico. El tiempo de concentración es un parámetro hidrológico, que representa el tiempo necesario para que toda cuenca, aporte en la generación del flujo en un punto emisor. Es decir, (Tc) representa la distribución en el tiempo del hidrograma de caudales, y permite estimar el caudal máximo de diseño para diferentes obras hidráulicas (Bentancor et al., 2014; Upegui & Gutiérrez, 2011). El (Tc) es el tiempo que demora una “gota de agua” en recorrer el punto más alejado de una cuenca a un punto emisor, no siempre corresponde al fenómeno real. Esto debido a que existen zonas, en los cuales la lluvia cae tarde y su recorrido es tardío al punto de desagüe, además este tiempo depende de las características geomorfológicas de cuenca y de la lluvia, y es propio de cada zona. Es conocido como el tiempo de respuesta o de equilibrio (Upegui & Gutiérrez, 2011). El tiempo de concentración es considerado como el tiempo de viaje, y es aplicable exclusivamente a la escorrentía superficial, es decir, la generada por la lluvia efectiva. Señala que en los libros de hidrología se ha establecido una frase poética tal como “una gota de agua de lluvia” en lugar de decir escorrentía superficial. Probablemente con la finalidad de asociar al tiempo de concentración con pequeñas inundaciones. Desde el punto de vista hidráulico, una gota de agua en una cuenca necesita un tiempo infinito para llegar al punto de salida en una cuenca (Michailidi et al., 2018). La frase “gota de agua” es irreal, debido a que el agua en suelo y en canales no existe como un conjunto de gotas. El agua en contacto con el suelo forma una masa amorfa. Señala que debemos de abandonar esa frase y establecer el comportamiento de la respuesta del agua en la masa amorfa (Beven, 2020). El tiempo de concentración es el intervalo de tiempo entre el fin de la lluvia efectiva y termino del escurrimiento superficial directa (Silveira, 2005). El tiempo de concentración varía según la intensidad de la lluvia y la humedad del suelo (Kirpich, 1940). Para cuencas muy grandes no se cumple la hipótesis de uniformidad en la lluvia. Para este caso se considera el tiempo de concentración como un tiempo representativo del flujo de las laderas más el tiempo de viaje de flujo en los cauces (Smith & Otalvaro, 1997). El tiempo de concentración es el parámetro temporal hidrológico más importante para lograr caracterizar y predecir las respuestas de una unidad hidrográfica frente a lluvia determinada (Almeida et al., 2022; Azizian, 2018). El tiempo de concentración es una fase de un aguadero que establece el caudal máximo, y que puede ser igual o no a la duración del aguacero. Esto debido a que el aguacero depende de variables climáticas y no del área de la cuenca. Las lluvias que generan los caudales máximos están relacionadas con el intervalo más intenso de la lluvia (Témez Peláez, 2003). Este tiempo se encuentra entre el final de la precipitación efectiva y al final de la escorrentía superficial directa (Taylor & Schwarz, 1952). No es la velocidad del flujo de área lo que define el tiempo de respuesta de una cuenca. Es la celeridad de flujo o velocidad de onda, la cual es más rápida que la velocidad promedio del flujo de un área (Laurenson, 1964). El tiempo de concentración es el tiempo de viaje de una onda, desde el punto más alejado hidráulicamente de una superficie hasta un determinado punto (Chong et al., 2019). El tiempo de concentración está relacionado con la duración de la lluvia, el tamaño de la cuenca y la magnitud de la inundación (Westra et al., 2014). Las características físicas de una cuenca son: longitud, pendiente, forma y tamaño. Siendo la longitud del cauce principal el que mejor explica el comportamiento del tiempo de concentración. Por otro lado, la segunda característica más importante para estimar el tiempo de concentración es la pendiente, por ser la más utilizada en las ecuaciones de tiempo de concentración (Sheridan, 1994). Los parámetros morfométricos de relieve son elementos condicionantes en la estimación de tiempos de concentración y en la generación de crecidas de caudales pico de corta o extensa duración en cauces naturales. También influyen en el comportamiento torrencial de caudales dentro de una unidad hidrográfica (Méndez Mata, 2016). Determinaron que el tiempo de concentración varía con la intensidad de la lluvia y la humedad del suelo, pero como las lluvias carecían de precisión, consideró constante para todas las lluvias (Ramser, 1927; Kirpich, 1940). Sin embargo, se debe de entender que el tiempo de concentración no es constante (Upegui & Gutiérrez, 2011). No existe una regla general o un método exacto para lograr estimar el tiempo de concentración en un punto de una cuenca. Estos tiempos fueron determinados a partir de ajustes empíricos (McCuen et al., 1984; Castillo et al., 2021). Existen dos grupos de métodos empíricas, las utilizadas en el diseño hidrológico y las de evento (Upegui & Gutiérrez, 2011). En la investigación se aplicó métodos empíricos para estimar el tiempo de concentración para la cuenca alta del Jequetepeque. El objetivo de la investigación fue verificar el desempeño de métodos empíricos para calcular el tiempo de concentración den la cuenca alta del “Jequetepeque”.
METODOLOGÍA
Zona de estudio
Las características morfológicas de la cuenca alta (Figura 1), condicionan el comportamiento del régimen hidrológico de caudales del cauce principal. Las nacientes de agua de la cuenca en estudio están marcadas por ríos perennes y quebradas efímeras. La zona alta presenta características de alta montaña, esto genera caudales torrentosos. Tanto las características físicas y las pendientes del cauce cambian en el curso del río Jequetepeque hasta su desem-bocadura en el Océano Pacífico. Las aguas de la cuenca pertenecen a la vertiente del Pacífico y son cosechadas en el embalse Gallito Ciego. La respuesta de escorrentía de la cuenca alta del Jequetepeque frente al régimen hidrológico de lluvias, se evidencian en el uso consuntivo y no consuntivo en la parte media y baja de la cuenca de estudio. Los caudales de cauce son registrados en la estación hidrométrica Yonán.
Parámetros geomorfológicos de la cuenca alta del Jequetepeque
Se utilizó modelos digitales de elevación (DEM) de 12,5 m de precisión de ALOS PALSAR. Se uso el software libre Qgis 2,18, para estimar los parámetros geomorfológicos de la cuenca alta de la cuenca del Jequetepeque. Estos parámetros fueron utilizados en los 32 métodos empíricos utilizados en la investigación, cuyas variables están relacionados con el área (km2), longitud de cauce principal (km) y pendiente (m/m), coincidiendo con Yoo et al. (2019) quienes señalan que la mayoría de métodos empíricos están en función de la longitud (L) y pendiente (S). Asimismo, los mencionados métodos presentan variables relacionados al número de curva y coeficiente de escorrentía, ver Tabla 2.
Métodos empíricos para el cálculo del tiempo de concentración
Los modelos empíricos son las más utilizadas en la práctica de la ingeniería (Mata-Lima et al., 2007). Los modelos empíricos también pueden consi-derarse como modelos deterministas (Gericke & Smithers, 2014). Los métodos empíricos de tiempo de concentración, son expresiones matemáticas obtenidas a partir de regresiones y correlaciones (Castillo et al., 2021). Los autores de los modelos empíricos, crearon modelos bajo las características particulares de cada cuenca (Upegui & Gutiérrez, 2011). Se seleccionaron 32 métodos empíricos.
a) Método de Kirpich
Este método fue propuesto en 1940 y utilizó seis pequeñas cuencas rurales para desarrollar su fórmula. Asimismo, se basó en el trabajo de 1927 de Ramser (Mota, 2012). Este método se desarrolló para cuencas agrícolas pequeñas, originalmente se aplicó a seis cuencas pequeñas en Tennessee y Pensilvania, Estados Unidos, basado en áreas de 0,00404685642 a 0,453247919 km2 y con pendientes entre 3 a 12% (Li & Chibber, 2008; Upegui & Gutiérrez, 2011; Sharifi & Hosseini, 2011). El modelo de Kirpich es el más utilizado mundialmente (Azizian, 2018). Se planteó dos expresiones:
Método de Kirpich-Tennessee
![]() (1)
(1)
Método de Kirpich- Pennsylvania
![]() (2)
(2)
Donde: L(km), S(m/m), tc (h)
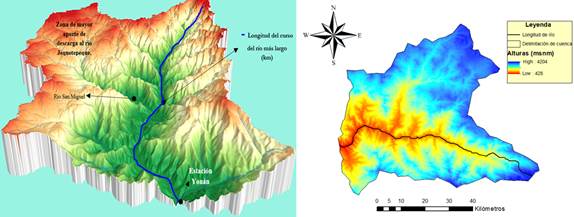
Figura 1. Longitud del cauce principal de la cuenca alta del Jequetepeque - (Perú).
b) Método de Témez
Este método fue propuesto en 1978 y fue probado en algunas cuencas de España, es recomendado para cuenca naturales con un área de hasta 300 103 Ha (3000km2) (Mata-Lima et al., 2007; Almeida et al., 2022)
![]() (3)
(3)
Donde: L(km), S(m/m), tc (h)
c) Método de Johnstone & Cross
Este método fue propuesto en 1949 y fue desarrollado con información de 19 cuencas rurales en la región de río Scioto- Sandusky, Estados Unidos. Con áreas de 64,8 a 4206,1 km2 (Silveira, 2005; Almeida et al., 2022; Mota, 2012)
![]() (4)
(4)
Donde: L(km), S(m/m), tc (h)
d) Método de Giandotti
Este método fue propuesto en 1934 y fue desarrollado a partir de información de cuencas italianas de la zona central y norte. Se recomienda utilizar este método para cuenca con áreas de 170 a 70000 km2 (Almeida et al., 2022; Mata-Lima et al., 200722; Alamri et al., 2023; Silveira, 2005; Azizian, 2018).
![]() (5)
(5)
Donde: L(km), S(m/m), A(km2), tc (h)
e) Método de Clark
Upegui & Gutiérrez (2011), menciona el siguiente método empírico:
![]() (6)
(6)
Donde: S(m/m), A(km2), tc (h)
f) Método de Ven te Chow
Este método fue propuesto en 1962 y fue desarrollado empíricamente a través de regresión al oeste de los Estados Unidos, y se tomó datos de veinte pequeñas cuencas, con áreas de 0,01-18,5 km2 y poca pendiente de 9 – 0,51% (Mota, 2012; Almeida et al., 2022; Azizian, 2018)
![]() (7)
(7)
Donde: L(km), S(m/m), tc (h)
g) Método del Cuerpo de ingenieros USA
Este método fue propuesto en 1954, y fue desarrollado en Estados Unidos. Para desarrollar este modelo, se utilizó 25 cuencas rurales, se recomienda utilizar este modelo para cuenca con áreas menores o iguales a 12000 km2 (Almeida et al., 2022; Azizian, 2018; Nagy et al., 2016; Silveira, 2005).
![]() (8)
(8)
Donde: L(km), S(m/m), tc (h)
h) Método de Haktanir & Sezen
Este método fue propuesto en 1990, y para desarrollar este modelo se utilizó diez cuencas en Turquía, se recomienda utilizar este modelo para cuenca con áreas entre 11- 9867 km2 (Almeida et al., 2022; Alamri et al., 2023; Azizian, 2018).
![]() (9)
(9)
Donde: L(km), tc (h)
i) Método de Epsey
Este método fue propuesto en 1966. Para desarrollar este modelo se utilizó once cuencas rurales en Estados Unidos (Mata-Lima et al., 2007; Alamri et al., 2023; Azizian, 2018; Almeida et al., 2022)
![]() (10)
(10)
Donde: L(km), S(m/m), tc (h)
j) Método de la Agencia Federal de Aviación, FAA
Este método fue propuesto en 1970 y fue desarrollado para ser empleadas en cuencas urbanas. Desarrollado a partir de información de drenaje de aeropuertos por el cuerpo de ingenieros de los Estados Unidos (Upegui & Gutiérrez, 2011; Almeida et al., 2022); Li & Chibber, 2008). Este método es uno de los métodos más utilizados en áreas urbanizadas (Silveira, 2005; Alamri et al., 2023)
![]() (11)
(11)
Donde: Coeficiente de escorrentía (C), L(km), S(m/m), tc (h)
k) Método de Ecuación de retardo, SCS
Este método fue propuesto en 1972 y fue desarrollado por el Servicio Conservación del Suelo de Estados Unidos (Soil Conservation Services) en Estados Unidos, aplicado a 24 pequeñas cuencas rurales de uso agrícola menores a 8 km2. Se ha demostrado que esta ecuaciones da buenos resultados en áreas completamente pavimentada (Li & Chibber, 2008; Silveira, 2005; Azizian, 2018; Almeida et al., 2022; Alamri et al., 2023)
![]() (12)
(12)
Donde: Coeficiente de escorrentía (C), Número de curva (NC), L(km), S(m/m), tc (h)
l) Método de Bransby-Williams (ASDOT)
Este método fue propuesto en 1995 y fue desarrollado en una zona tropical al este de la India. Este método empírico es aplicable para cuencas rurales menores a 130 km2. Esta expresión propuesta por The Institution Engineers de Australia, en reemplazo de la ecuación de Kirpich (1940) por estimar valores muy bajos. Así mismo, se recomienda utilizar esta fórmula para cuencas menores a 75 km2 (Upegui & Gutiérrez, 2011; Li & Chibber, 2008; Azizian, 2018; Castillo et al., 2021;Mata-Lima et al., 2007; Almeida et al., 2022).
![]() (13)
(13)
Donde: L(km), S(m/m), A(km2), tc (h)
m) Método de práctica de alcantarillas de California
Este método fue propuesto en 1955. Es una expresión modificada de la ecuación de Kirpich. Este método utilizó datos de pequeñas cuencas montañosas de California en Estados Unidos y es la expresión oficial para estimar el tiempo de concentración en el drenaje pluvial. (Sharifi & Hosseini, 2011; Almeida et al., 2022; Mata-Lima et al., 2007;Castillo et al., 2021; Azizian, 2018). Este método tiene un amplio uso, así como las fórmulas de Izzard, Kirpich entre otros (Rodríguez López & Marrero de León, 2015)
![]() (14)
(14)
Donde: L(km), S(m/m), tc (h)
n) Método de Pilgrim & McDermott
Este método fue propuesto en 1982. Se recomienda utilizar esta fórmula para cuencas menores a 250 km2. Desarrollado a partir de 96 cuencas en el este de Nueva Gales del Sur (Upegui & Gutiérrez, 2011; Azizian, 2018).
![]() (15)
(15)
Donde: A(km2), tc (h)
o) Método de Snyder
Este método fue propuesto en 1938 y fue desarrollado en Estados Unidos, en las zonas altas de los Apalaches. Este método fue utilizado en 20 cuencas, en cuencas cuyas áreas son de 25 a 25000 km2 (Sultan et al., 2022; Upegui & Gutiérrez, 2011).
![]() (16)
(16)
Donde: Lcg (mi), L(km), tc (h)
p) Método de Valencia & Zuluaga
Upegui & Gutiérrez (2011), menciona el siguiente método empírico:
![]() (17)
(17)
Donde: S0(%), L(Km), A(Km2), tc (h)
q) Método de Carter
Este método fue propuesto en 1961 y fue desarrollado con información de cuencas urbanas en Estados Unidos, para áreas menores a 20.7199049 km2, para una longitud de canal menor a 11,265408 km y pendiente menores a 0,005 (Sharifi & Hosseini, 2011; Almeida et al., 2022).
![]() (18)
(18)
Donde: L(Km), S(m/m), tc (h)
r) Método de Pasini
Este método fue propuesto en 1914 y fue desarrollado con información de cuencas rurales en Italia con poca pendiente (Mata-Lima et al., 2007; Almeida et al., 2022; Mota, 2012).
![]() (19)
(19)
Donde: A(Km2), L(Km), S(m/m), tc (h)
s) Método de Ventura
Recomendado por la Escuela Nacional de Puentes Chaussées (Francia). Desarrollado con información de cuencas rurales en el valle del Po, Italia (Sultan et al., 2022; Mata-Lima et al., 2007; Silveira, 2005; Almeida et al., 2022).
![]() (20)
(20)
Donde: L(Km), A(Km2), H(m), tc (h)
t) Método de Dooge
Este método fue propuesto en 1973. Fue O’Kelly en el año de 1955, quien desarrolló una primera versión de la fórmula propuesta por Dooge, a partir de información de diez cuencas rurales en Irlanda, con áreas de 145 – 948 km2. Finalmente Dooge (1973) dedujo la siguiente fórmula, (Mota, 2012; Silveira, 2005; Almeida et al., 2022)
![]() (21)
(21)
Donde: A(Km2), S(m/m), tc (h)
u) Método de Simas - Hawkins
Este método fue propuesto en 1996 y fue desarrollado en los Estados Unidos, usaron información de 168 cuencas, con rango de áreas de 0,001 -14 km2 (Almeida et al., 2022).
![]() (22)
(22)
Donde: L(Km), A(Km2), S(m/m), tc (h), Número de curva (NC).
Las fórmulas mencionadas representan al tiempo de concentración (tc), expresados en (horas). Las variables de las 32 fórmulas están relacionadas con: L es la longitud del curso del río más largo (km), H es la diferencia de alturas entre la divisoria de aguas y el punto de salida (m), S es la pendiente del cauce principal (m/m), S0 es la pendiente expresada en porcentaje, A es el área de la unidad hidrográfica (km2), Lcg es la distancia desde la salida hasta el centro de gravedad de la cuenca expresados en millas (mi), NC es el número de curva, C es el coeficiente de escorrentía. Según Yoo et al. (2019) y Alamri et al. (2023), las fórmulas presentadas en la Tabla 1, derivan de investi-gaciones y experimentos en cuencas con condiciones climáticas particulares.
Tabla 1
Expresiones de tiempos de concentración
|
Método |
Fórmula |
N° |
Método |
Fórmula |
N° |
|
JSCE (1999) |
|
(23) |
Rziha (1876)
|
|
(28) |
|
MOCT (1974)
|
|
(24) |
Alamri (2023) |
|
(29) |
|
Ahn & Lee (1986) |
|
(25) |
USGS (2000)
|
|
(30) |
|
Yoon & Park (2002)
|
|
(26) |
Jung (2005)
|
|
|
|
Kim (2015)
|
|
(27) |
Albishi (2017)
|
|
(31) |
Fuente: (Yoo et al., 2019; Alamri et al., 2023).
La Tabla 1, presenta métodos empíricos y el año de propuesta, en función de (A) área (Km2), (S) pendiente (m/m), y (L) longitud de cauce principal (Km), estos son: JSCE (1999), Rziha (1876), MOCT (1974), Alamri (2023), Ahn & Lee (1986), USGS (2000), Yoon & Park (2002), Jung (2005), Kim (2015) y Albishi (2017) (Alamri et al., 2023; Yoo et al., 2019). Por otro lado, Yoo et al. (2019) señala que las fórmulas siguientes están relacionadas con la longitud y pendiente: Kirpich (1940), Izzard y Hicks (1947), Johnstone y Cross (1949), Kerby (1959), Carter (1961), Morgali y Linsley (1965), Espey y Winslow (1974), SCS (1975). Asimismo, señala que las siguientes formulas, tales como: Kirpich-Tennessee en 1940, Kraven (I) (JSCE 1999), California (1955), SCS (1975), Carter (1961), MOCT (1974), Espey & Winslow (1974) fueron creadas para cuencas empinadas con características de lluvias intensas. Además, señala que la expresión de Johnstone and Cross (1949) fue desarrollado para ríos con flujo laminar. Por otro lado, las expresiones de Agencia Federal de Aviación, FAA (1970), Rziha (1876) y ecuación de retardo, SCS (1972) fueron desarrolladas para flujo de ríos con flujo laminar y turbulento. Michailidi et al. (2018), señala que los métodos empíricos tradicionales, tales como: Giandotti (1934), Kirpich (1940) y SCS (1975) están relacionan con características geomorfológicas (área, pendiente y longitud de río) ignorando la velocidad.
Estimación del tiempo de concentración
En la hidrología, se estima el tiempo de concen-tración con metodologías determinísticas, se obtiene el promedio de los valores estimados por diferentes métodos, luego se separa los valores extremos de tiempos de concentración, por estar fuera de la media. Posteriormente se saca la media de los valores resultantes, señalada por Martínez (2005). Para estimar el tiempo de concentración es adecuado contar con la mayor cantidad de modelos empíricos, ya que de esta manera se reduce la incertidumbre de selección (Upegui & Gutiérrez, 2011). Es conveniente incluir por lo menos cinco modelos empíricos diferentes para obtener la media para la estimación del tiempo de con-centración (Bodhinayake, 2004). Coincidiendo con Vélez et al. (2013) indican que los investigadores como Chow et al., 1994, Smith & Vélez, 1997, Linsley et al., 1990, Viessman & Lewis, 2003, y Vélez & Botero, 2011, señalan que para observar el tiempo de respuesta de la cuenca es necesario contar con varias ecuaciones, siendo apropiado contar con por lo menos cinco estimaciones de diferente valor. Para la estimación del tiempo de concentración de la cuenca alta del Jequetepeque (Figura 1) se utilizó 32 métodos empíricos, cuyas variables están relacionadas con parámetros geomorfológicos de la cuenca en estudio (Tabla 2).
Se identificó de la cuenca alta del Jequetepeque la zona de recarga correspondiente a la cuenca de san Miguel. Además, en el relieve topográfico de la cuenca alta del Jequetepeque, se ubicó el tramo del río más largo de la cuenca alta, ver Figura 1, Tabla 2. Se obtuvo información morfológica de la cuenca en estudio, utilizando sistema de información geográfica (SIG), tal como se presenta en la Tabla 2. Esta información es la base para el cálculo del tiempo de concentración relacionados a paráme-tros geomorfológicos.
Los métodos determinísticos aplicados en la inve-stigación para obtener el tiempo de concentración fueron desarrollados para cuencas urbanas y rurales. Estos valores son expresados en horas, y fueron estimados a partir de 32 diferentes métodos determinísticos.
La Tabla 3 presentan 32 resultados diferentes tiempos de concentración, los cuales fueron obtenidos en función de los parámetros morfológicos de la cuenca en estudio.
Algunos modelos presentados en la Tabla 1, no especifican las características de uso. Sin embargo, algunos métodos derivan de investigaciones y experimentos realizadas en cuencas con condiciones climáticas particulares (Yoo et al., 2019). El estudio geodinámico de la cuenca del río Jequetepeque - [Boletín C 10] realizado por el Instituto Geológico, Minero y Metalúrgico (INGEMMET), señala que el tiempo de concentración para la cuenca del río Jequetepeque, presenta un rango entre 6 y 12 horas (Lionel et al., 1994).
Tabla 2
Parámetros geomorfológicos de la cuenca alta del Jequetepeque
|
Valor /Característica |
||
|
Punto de control (PC) |
Estación hidrométrica Yonán |
Unidad |
|
Área de drenaje (A) |
3288,81 |
km2 |
|
Pendiente de cauce principal (S) |
13,93 |
% |
|
Pendiente de cauce principal (S0) (en tanto por uno) |
0,0383 |
m/m |
|
Longitud de cauce principal (L) |
95,94 |
km |
|
Cota máxima de longitud de cauce (H máx) |
4146,33 |
msnm |
|
Cota mínima de longitud de cauce (H min) |
469,37 |
msnm |
|
Coeficiente de escorrentía (C) |
0,65 |
- |
|
Numero de curva (NC) |
77,65 |
- |
|
Distancia desde la salida hasta el centro de gravedad de la cuenca (LCG) |
45,36 |
km |
|
Distancia desde la salida hasta el centro de gravedad de la cuenca (LCG) |
28,19 |
mi |
Tabla 3
Tiempos de concentración mediante modelos determinísticos
|
Tc (h) |
|
|
Kirpich-Tennessee (1940) |
7,82 |
|
Kirpich- Pennsylvania (1940) |
1,89 |
|
Témez (1978) |
17,89 |
|
Johnstone and Cross (1949) |
10,23 |
|
Giandotti (1934) |
10,88 |
|
Clark |
107,31 |
|
Ven te Chow (1962) |
8,44 |
|
Cuerpo de ingenieros USA (1954) |
11,39 |
|
Haktanir & Sezen |
34,70 |
|
Epsey |
64,08 |
|
Agencia Federal de Aviación, FAA (1970) |
4,93 |
|
Ecuación de retardo, SCS (1972) |
192,45 |
|
Bransby-Williams |
19,74 |
|
Práctica de alcantarillas de California (1955) |
7,84 |
|
Pilgrim & McDermott |
16,49 |
|
Snyder (1938) |
12,85 |
|
Valencia & Zuluaga |
7,39 |
|
Carter (1961) |
4,02 |
|
Pasini (1914) |
37,40 |
|
Ventura |
37,05 |
|
Dooge (1973) |
17,58 |
|
Simas - Hawkins (1996) |
16,94 |
|
JSCE (1999) |
3,81 |
|
Rziha (1876) |
9,44 |
|
MOCT (1974) |
37,19 |
|
Almri (2023) |
23,73 |
|
Ahn & Lee (1986) |
50,24 |
|
USGS (2000) |
150,72 |
|
Yoon & Park (2002) |
6,87 |
|
Jung (2005) |
8,24 |
|
Kim (2015) |
6,16 |
|
Albishi (2005) |
2,97 |
|
Promedio |
29,65 |
|
Máximo |
192,44 |
|
Mínimo |
1,89 |
Según Upegui & Gutiérrez (2011), las estimaciones de tiempo de concentración generan diferentes resulta-dos, debido a que cada método fue creado para una cuencas específicas y características únicas. Se aplicó la metodología señalada por Martínez (2005). De los 32 valores de la Tabla 3, se obtuvo un promedio igual a 29,65 horas. Se eliminó los valores más distanciados con respecto al promedio indicado, estos métodos fueron: Clark, Haktanir & Sezen, Epsey, Ecuación de retardo SCS (1972), Pasini (1914), Ventura, MOCT (1974), Ahn & Lee (1986), USGS (2000) y la Agencia Federal de Aviación, FAA (1970). Además, se descar-taron los valores mínimos obtenidos de los métodos Kirpich-Pennsylvania (1940), Carter (1961), JSCE (1999) y Albishi (2005). Los valores eliminados de tiempo de concentración se encuentran fuera del rango de valores señalados por Lionel et al. (1994). Si se usan tiempos de concentración sobreestimados, se sobreestima el caudal máximo, lo cual genera un sobredimensionamiento tanto en la infraestructura hidráulica como en el costo del material de cons-trucción. Se debe tener cuidado en la selección de los métodos empíricos cuando se utilizan fuera de las regiones de donde fueron desarrollados. Si se toman estos métodos de tiempos de concentración sin previa evaluación, se sobre o subestimaría el caudal máximo para cualquier tiempo de retorno, lo cual generaría problemas en el diseño y funcionamiento (Sultan et al. 2022). Coincidiendo con Gericke & Smithers (2014) quienes señalan que una mala estimación de tiempo de concentración traería problemas en lo socioe-conómico de proyectos agrícolas.
Se aplicó la metodología señalada por Martínez (2005). De los valores de tiempo de concentración restantes, se obtuvo un promedio igual a 12,22 horas. Se tomó este valor, y eliminó los valores más alejados al promedio, estos métodos fueron: el método de Témez (1978), Bransby-Williams, Pilgrim, McDermott, Snyder (1938), Dooge (1973), Simas-Hawkins (1996) y Alamri (2023). Asimismo, para poder elegir posibles valores a de tiempos de concentración, se consideró lo indicado por (Lionel et al., 1994), respecto al rango del tiempo concen-tración para la cuenca del Jequetepeque (6 -12 h). De los métodos restantes, se obtuvo un promedio igual a las 8,61 horas, y se aplicó la metodología señalada por Martínez (2005). En este caso, no se eliminaron los valores más distanciados con respecto al promedio del tiempo de concentración. Esto es debido, a que los valores de los métodos (Figura 2) están contemplados dentro del rango de valores de tiempo de concentración (6 -12 h) planteados por (Lionel et al., 1994) para la cuenca del Jequetepeque.
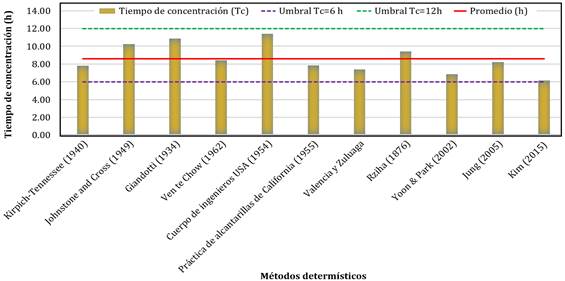
Figura 2. Umbral y promedio del tiempo de concentración de la cuenca en estudio.
Se consideró lo establecido por Upegui & Gutiérrez (2011), quien señalo que es adecuado contar con la mayor cantidad de modelos determinísticos, ya que de esta manera se reduce la incertidumbre de selección del valor de tiempo de concentración. Se tomó en cuenta lo dicho por Bodhinayake (2004), quien señala que, para estimar el tiempo de concentración, por lo menos debemos incluir cinco modelos diferentes para obtener la media de los valores del tiempo de concentración. Finalmente, el resultado obtenido muestra mayor respaldo con Vélez et al. (2013) al señalar que varios investi-gadores como Chow et al. (1994), Smith & Vélez (1997), Linsley et al. (1990), Viessman & Lewis (2003), y Vélez & Botero (2011), recomiendan utilizar varias ecuaciones para estimar el tiempo de concentración de respuesta de la cuenca, siendo apropiado contar con por lo menos cinco estima-ciones. En esta etapa de la investigación se consideró a los modelos determinísticos relacio-nadas a cuenca rurales o de montaña, tales como: Kirpich-Tennessee (1940), Johnstone & Cross (1949), Giandotti (1934), Ven te Chow (1962), Cuerpo de ingenieros USA (1954), Práctica de alcantarillas de California (1955), Valencia & Zuluaga, Rziha (1876), Yoon & Park (2002), Jung (2005) y Kim (2015). Los mencionados modelos fueron desarrollados para cuencas rurales, cuyo rango de estimación de valores esta entre los 6,16 horas y 11,39 horas. Cabe mencionar que los métodos de Epsey, Agencia Federal de Aviación, FAA (1970) y Carter (1961) son usados para cuencas urbanas.
En cuencas con pequeñas áreas, la distribución de precipitación pluvial es homogénea. A diferencia de las cuencas grandes, cuya precipitación pluvial areal no es homogénea. La orografía cercana a la cordillera de los andes y la cobertura vegetal de la unidad hidrográfica en estudio, influye en el comportamiento del régimen de precipitaciones (lluvia). Según Westra et al. (2014) las caracte-rísticas espaciales y temporales de la lluvia influyen tanto en cuenca pequeñas como en cuenca más grandes. En una cuenca pequeña las tormentas de lluvia son cortas pero intensas, que pueden durar solo una hora o quizás menos, Pero en una cuenca más grande las tormentas de lluvias son más prolongados, estas lluvias son intensas y puede durar días o más. Según Upegui & Gutiérrez (2011), en cuencas muy grandes no se cumple la distribución uniforme de lluvias sobre toda la superficie de una cuenca, Por tanto, se toma al tiempo de concentración como un tiempo representativo del tiempo de viaje del flujo en laderas y el tiempo de viaje del flujo en cauces (riachuelos). Según Sandoval (2022), estas variables están consideradas en la norma Rusa SP-33-101-2003, donde relacionan al tiempo de concentración (Tc) con las variables de tiempo de flujo laminar de ladera TL y el tiempo de recorrido en cauces (riachuelos) Tr. En los métodos presentados no se consideró el TL, Tr y la vegetación, debido a que todos los modelos utilizados en la investigación son los más usados en la determinación del tiempo de concentración y están relacionados con parámetros morfométricos. Según Mota (2012),existe una mayor dificultad en obtener información hidrológica de una cuenca, que información de datos morfométricos. Sandoval & Aguilera (2015) indican en base a lo propuesto por Goroshkov en el año de 1979 que, para una cuenca mediana o grande, el tiempo de recorrido de flujo de cauces y el tiempo de flujo de laderas, será menor o igual a 10 min. Por lo tanto, el valor del tiempo de concentración será considerado del cauce principal. Según lo señalado, se clasificó a la cuenca en estudio (área igual a 3288,81 km2), a través de la clasificación de cuencas de Campos (1998), y se concluyó que la cuenca alta del Jequetepeque, es un cuenca grande. Por tanto, según lo indicado, podemos señalar que el tiempo de concentración para la cuenca alta del Jequetepeque, será tomado del cauce principal, con un valor igual a 8,61 h. McCuen et al. (1984) señalan que para un área de 16,187 km2 el tiempo de concentración es de 1,49 horas, deduciendo que, mientras más grande es el área, el tiempo de concentración será también proporcional. Según Beven (2020), la ventaja de utilizar métodos simples, es que los parámetros de los métodos señalados en la Tabla 3, se ajustan a las características de la cuenca. El tiempo de concentración, permite estimar hidrogramas unitarios para cuencas no aforadas, en base a parámetros derivados de cuencas. Para Hotchkiss & McCallum (1995) este parámetro es de mucha importancia en muchos métodos de caudal máximo, para evitar inundaciones y garantizar un diseño hidráulico económico.
La investigación partió de la siguiente hipótesis, el cual señala que el modelo de Kirpich- Pennsylvania es el modelo determinista de cuantificación del tiempo de concentración para la cuenca en estudio, esto a raíz de ser el método más utilizado. Siendo rechazada esta hipótesis, por subestimar el tiempo de concentración con respecto al rango de tiempo de concentración establecido por (Lionel et al., 1994), cuyo rango de tiempo de concentración es de 6 a 12 horas para la cuenca en estudio. Finalmente se establece que el desempeño de los modelos deterministas está en función del uso parámetros morfométricos de la cuenca en estudio, siendo el tiempo de concentración igual a 8,61 horas (516,6 min).
El Perú cuenta con una diversidad de cuencas de diversos tamaños, donde el tiempo de concentración se establece con modelos determinísticos (empíricos), desarrollados con las características climáticas y geomorfológicas de otros países. Para cuencas con nula información de precipitación pluvial, los métodos determinísticos estudiados, desempeñan un papel fundamental en la estimación del tiempo de concentración, ya que sus variables relacionadas con los parámetros geomorfológicos de una cuenca son fáciles de obtener. Asimismo, estos modelos determinísticos no permiten cuantificar el tiempo de concentración a tiempo real, pero si logran dar un valor próximo a partir de las características morfométricas de la cuenca. Para los hidrólogos, el tiempo de concen-tración es el parámetro más importante para estimar caudales máximos. Los valores estimados por Kirpich-Tennessee (1940), Johnstone and Cross (1949), Giandotti (1934), Ven te Chow (1962), Cuerpo de ingenieros USA (1954), Práctica de alcantarillas de California (1955), Valencia & Zuluaga, Rziha (1876), Yoon & Park (2002), Jung (2005), Kim (2015), se encuentran dentro del rango del tiempo de concentración (tc) 6 a 12 horas, de la cuenca en estudio. A su vez el promedio de dicho rango del tiempo de concentración para la cuenca alta del Jequetepeque (9 horas), es próximo al promedio del tiempo de concentración estimado por los métodos empíricos mencionados anterior-mente (8,61 horas). Además, los métodos seña-lados representan el 34% del total de los modelos estudiados. Cabe señalar que los métodos de Ven te Chow (1962), Jung (2005) y Rziha (1876) estimaron valores de tiempo de concentración próximo al promedio del rango de tiempo de concentración propuesto por (Lionel et al., 1994).
REFERENCIAS BIBLIOGRÁFICAS
Alamri, N., Afolabi, K., Ewea, H., & Elfeki, A. (2023a). Evaluation of the Time of Concentration Models for Enhanced Peak Flood Estimation in Arid Regions. Sustainability, 15(3), 1987. https://doi.org/10.3390/SU15031987
Almeida, A. K., de Almeida, I. K., Guarienti, J. A., & Gabas, S. G. (2022). The time of concentration application in studies around the world: a review. Environmental Science and Pollution Research, 29(6), 8126–8172. https://doi.org/10.1007/s11356-021-16790-2
Azizian, A. (2018). Uncertainty Analysis of Time of Concentration Equations based on First-Order-Analysis (FOA) Method. American Journal of Engineering and Applied Sciences, 11(1), 327–341. https://doi.org/10.3844/ajeassp.2018.327.341
Bentancor, L., Silveira, L., & García Petillo, M. (2014). Incidencia de la intensidad de lluvia en el tiempo de concentración de microcuencas del Uruguay. Agrociencia, 18(2), 106–116. https://doi.org/10.31285/agro.18.471
Beven, K. J. (2020). A history of the concept of time of concentration. Hydrology and Earth System Sciences, 24(5), 2655–2670. https://doi.org/10.5194/HESS-24-2655-2020
Bodhinayake, N. D. (2004). Influence of hydrological, geomorphological and climatological characteristics of natural catchments on lag parameters. PhD thesis, School of Civil, Mining and Environmental engineering, University of Wollongong. https://ro.uow.edu.au/theses/385/
Bondelid, T. R., McCuen, R. H., & Jackson, T. J. (1982). Sensitivity of SCS Models to Curve Number Variation. Journal of The American Water Resources Association, 18(1), 111–116. https://doi.org/10.1111/J.1752-1688.1982.TB04536.X
Campos, D. F. (1998). Procesos del ciclo hidrológico. UASLP. San Luis Potosí, México, 20. https://repositorioinstitucional.uaslp.mx/xmlui/handle/i/3331
Castillo García, C. L., Abreu Franco, D. E., & Alvarez González, M. (2021a). Evaluación de distintas fórmulas empíricas para el cálculo del tiempo de concentración en la cuenca urbana del río Bélico y Cubanicay, ciudad de Santa Clara. Enfoque UTE, 12(3). https://doi.org/10.29019/enfoqueute.729
Chong, K. L., Nifa, F. A. A., Nawi, M. N. M., Sayama, T., Takara, K., & Abustan, I. (2019). Ecological effects of hydrological process on time of concentration. Ekoloji, 28(107), 1437–1443.
Gericke, O. J., & Smithers, J. C. (2014). Revue des méthodes d’évaluation du temps de réponse d’un bassin versant pour l’estimation du débit de pointe. Hydrological Sciences Journal, 59(11), 1935–1971. https://doi.org/10.1080/02626667.2013.866712
Hotchkiss, R. H., & McCallum, B. E. (1995). Peak discharge for small agricultural watersheds. Journal of Hydraulic Engineering, 121(1).
Kirpich, Z. P. (1940). Kirpich: Time of concentration of small agricultural watersheds. Civil engineering, 10(6), 362.
Laurenson, E. M. (1964). A catchment storage model for runoff routing. Journal of Hydrology, 2(2), 141–163. https://doi.org/10.1016/0022-1694(64)90025-3
Lionel, I., Smoll, F., Pedro, I., & Ballena, O. (1994). Estudio geodinámico de la cuenca del río Jequetepeque - [Boletín C 10]. Instituto Geológico, Minero y Metalúrgico - INGEMMET. https://repositorio.ingemmet.gob.pe/handle/20.500.12544/271
Martínez Álvarez, V. (2006). Determinación del tiempo de concentración con sistemas de información geográfica. Ingeniería del agua, 13(4), 303-309. https://doi.org/10.4995/ia.2006.10495
Martínez, E. (2005). Hidrología práctica. España. Editorial del Colegio de Ingenieros de Caminos, Canales y Puertos. Madrid. 317 p.
Mata-Lima, H., Vargas, H., Carvalho, J., Gonçalves, M., Caetano, H., Marques, A., & Raminhos, C. (2007). Comportamento hidrológico de bacias hidrográficas: integração de métodos e aplicação a um estudo de caso. Rem: Revista Escola de Minas, 60(3), 525–536. https://doi.org/10.1590/S0370-44672007000300014
McCuen, R. H., Wong, S. L., & Rawls, W. J. (1984). Estimating Urban Time of Concentration. Journal of Hydraulic Engineering, 110(7), 887–904. https://doi.org/10.1061/(ASCE)0733-9429(1984)110:7(887)
Méndez Mata, W. J. (2016). Análisis cuantitativo del relieve en cuencas de drenaje de la vertiente norte del macizo “El Ávila” (estado Vargas, Venezuela) y su significado hidrogeomorfológico. Investigaciones Geográficas, Boletín Del Instituto de Geografía, 2016(91), 25–42. https://doi.org/10.14350/RIG.47722
Michailidi, E. M., Antoniadi, S., Koukouvinos, A., Bacchi, B., & Efstratiadis, A. (2018). Timing the time of concentration: shedding light on a paradox. Hydrological Sciences Journal, 63(5), 721–740. https://doi.org/10.1080/02626667.2018.1450985
Mota, A. de A. (2012). Tempo de concentração em pequena bacia experimental [Florianópolis]. https://repositorio.ufsc.br/handle/123456789/100709
Nagy, E. D., Torma, P., & Bene, K. (2016). Comparing Methods for Computing the Time of Concentration in a Medium-Sized Hungarian Catchment. Slovak Journal of Civil Engineering, 24(4), 8–14. https://doi.org/10.1515/SJCE-2016-0017
Rodríguez López, Y., & Marrero de León, N. (2015). Simulación hidrológica en dos subcuencas de la cuenca del río Zaza de Cuba. Ingeniería Hidráulica y Ambiental, 36(2), 109–123.
Ramser, C. E. (1927). Run-off from small agricultural areas. Cir.Nii.Ac.Jp. https://cir.nii.ac.jp/crid/1572824500236025600
Sandoval, W. R., & Aguilera, E. P. (2015). Determinación de Caudales en cuencas con poco información Hidrológica. CIENCIA UNEMI, 7(12), 100–110. https://doi.org/10.29076/issn.2528-7737vol7iss12.2014pp100-110p
Sandoval. W. E (2022). Tiempo de concentración de una cuenca. Conference: Conferencia por loa 100 años de creación de la Carrera de Ingeniería Civil de la ESPE. http://dx.doi.org/10.13140/RG.2.2.28576.66565
Sharifi, S., & Hosseini, S. M. (2011). Methodology for Identifying the Best Equations for Estimating the Time of Concentration of Watersheds in a Particular Region. Journal of Irrigation and Drainage Engineering, 137(11), 712–719. https://doi.org/10.1061/(asce)ir.1943-4774.0000373
Sheridan, J. M. (1994). Hydrograph Time Parameters for Flatland Watersheds. Transactions of the ASAE, 37(1), 103–113. https://doi.org/10.13031/2013.28059
Silveira, A. L. L. da. (2005). Desempenho de Fórmulas de Tempo de Concentração em Bacias Urbanas e Rurais. RBRH. Revista Brasileira de Recursos Hidricos, 10(1), 5–29.
Smith, R., & Otalvaro, M. V. V. (1997). Hidrología de Antioquia. Secretaria de Obras Publicas Departamentales. 253 pp.
Sultan, D., Tsunekawa, A., Tsubo, M., Haregeweyn, N., Adgo, E., Meshesha, D. T., Fenta, A. A., Ebabu, K., Berihun, M. L., & Setargie, T. A. (2022). Evaluation of lag time and time of concentration estimation methods in small tropical watersheds in Ethiopia. Journal of Hydrology: Regional Studies, 40, 101025. https://doi.org/10.1016/J.EJRH.2022.101025
Taylor, A. B., & Schwarz, H. E. (1952). Unit‐hydrograph lag and peak flow related to basin characteristics. Eos, Transactions American Geophysical Union, 33(2), 235–246. https://doi.org/10.1029/TR033I002P00235
Témez Peláez, J. R. (2003). Facetas del cálculo hidrometeorológico y estadístico de máximos caudales. Revista de Obras Públicas, 3430, 47-51.
Velez, J. J., Botero, B. A., Parra, J. C., Aristizabal, V. M., & Marulanda, A. (2013). Diseño hidráulico e hidrológico de obras de ingeniería para proyectos viales. https://repositorio.unal.edu.co/handle/unal/82744
Upegui, J. J. V., & Gutiérrez, A. B. (2011). Estimación del tiempo de concentración y tiempo de rezago en la cuenca experimental urbana de la quebrada san luis, manizales. DYNA (Colombia), 78(165), 58–71.
Westra, S., Fowler, H. J., Evans, J. P., Alexander, L. V., Berg, P., Johnson, F., Kendon, E. J., Lenderink, G., & Roberts, N. M. (2014). Future changes to the intensity and frequency of short-duration extreme rainfall. Reviews of Geophysics, 52(3), 522–555. https://doi.org/10.1002/2014RG000464
Yoo, C., Lee, J., & Cho, E. (2019). Theoretical evaluation of concentration time and storage coefficient with their application to major dam basins in Korea. Water Science and Technology: Water Supply, 19(2), 644–652. https://doi.org/10.2166/ws.2018.156