Características acústicas de trece especies de maderas en la
fabricación de instrumentos musicales
Acoustic
characteristics of thirteen species of woods in the manufacture of musical
instruments
Jorge Omar Livia Calderón1;
Luis Shuseki Yoza Yoza2 *; Moisés Pascual Acevedo Mallque1
Rodolfo Sonco Cutire2;
Oscar Tang Cruz 2
1 Facultad de Ciencias Forestales, Dpto. Industrias
Forestales, Universidad Nacional Agraria La Molina, La Molina, Lima, Perú.
2 Facultad de Ciencias, Dpto. Física y Meteorología,
Universidad Nacional Agraria La Molina, La Molina, Lima, Perú.
* Autor corresponsal: Iyoza@lamolina.edu.pe (L. S. Yoza Yoza).
ORCID de los autores:
J. O. Livia Calderón: https://orcid.org/0000-0003-1685-9875 L.
S. Yoza Yoza: https://orcid.org/0000-0003-1540-182X
M. P. Acevedo
Mallque:
https://orcid.org/0000-0002-0638-395X R.
Sonco Cutire: https://orcid.org/0000-0001-5955-2174
O. Tang Cruz: https://orcid.org/0000-0002-4641-7368
RESUMEN
Se
evaluaron las propiedades acústicas en trece especies de madera, incluyendo maderas
tradicionales y maderas alternativas para ser utilizadas en la luthería. Se evaluaron:
la velocidad del sonido, el amortiguamiento de la radiación sonora, la
resistencia de la onda acústica, modos de vibración y el decaimiento
logarítmico vibracional. La selección de las especies de madera se realizó
mediante técnicas tradicionales aplicados por los luthieres, además de la
determinación de la densidad y la humedad de las maderas. El estudio empleó principalmente
técnicas acústicas no destructiva y comparó las respuestas acústicas en
muestras radiales y longitudinales. Los resultados comparados con las maderas
acústicas tradicionales; confirmaron que el Palisangre (Brosimun rubescens)
y palo azufre (Symphonia globulifera) presentan las mejores propiedades
acústicas deseables para la fabricación de instrumentos musicales, lo que
permite mejorar la elaboración de fondos y aros de resonancia de instrumentos musicales
a cuerda.
Palabras clave: luthier; maderas tonales; sonido; frecuencia
fundamental.
ABSTRACT
The acoustic
properties of thirteen species between traditional woods and alternative woods are
to be used in lathery. The following were evaluated: the speed of sound, the
damping of sound radiation, the resistance of the acoustic wave, vibration
modes and the logarithmic vibrational decay. The selection of wood species was
carried out using traditional techniques applied by luthiers, in addition to
determining the density and humidity of the wood. The study primarily employed
non-destructive acoustic techniques and compared acoustic responses in radial
and longitudinal samples. The results compared to traditional acoustic woods
confirmed that Palisangre (Brosimun rubescens) and palo Azufre (Symphonia
globulifera) present the best acoustic properties desirable for the
manufacture of musical instruments, which allows improving the elaboration of
backs and resonance sides of stringed musical instruments.
Keywords: chordophones;
luthier; wood tone; speed of sound; fundamental frequency.
Recibido: 29-10-2024.
Aceptado: 02-03-2025.
La
madera como material de ingeniería posee propie-dades físicas, mecánicas,
químicas; algunas de estas son más conocidas por su uso tradicional y otras
poco difundidas, como es el caso de las propiedades acústicas. La madera es la
materia prima tradicional utilizada para la elaboración de instrumentos musicales
por tener cualidades acústicas, es así que el conocimiento de estas propiedades de
la madera se considera como esencial para determinar un producto de mayor valor
y calidad, aprovechando así al máximo el recurso natural y proponiendo nuevas
especies para su uso. En este contexto, se puede analizar la madera por su
anisotropía, por sus modos mecánico-elásticos como el MOE el MOR y coeficiente
de Poisson. Por otro lado, del punto de vista energético, como: los de modos de
vibración ortogonales, de activación y decaimiento, de atenuación y absorción.
Además, en el caso de instrumento tipo cordófonos se caracterizan acústicamente
sus componentes como la tapa, fondo, aros, diapasón y otros. En el presente
trabajo se puede proponer la utilización de métodos no destructivos para
determinar la velocidad de las ondas mecánicas, densidad, los modos de
vibración de las muestras de maderas y su decaimiento logarítmico (De la
Cruz, 2018).
Cabe señalar que, en el Perú, la falta de información acerca de las propiedades
acústicas de la madera es una de las limitantes para su uso en la industria de
la construcción de instrumentos musicales, y que esta actividad se realiza de
forma artesanal; es necesario precisar que no todas las especies maderables
tienen propiedades acústicas óptimas, ni toda la madera de un árbol es
aprovechable en términos acústicos. En esta investigación la selección de las
especies de madera se realizó según los métodos tradicionales usados por los
luthieres; se evaluaron especies alternativas tropicales, y especies de uso
tradicional nacionales e importadas; El objetivo consistió en determinar las
propiedades mecánicas elásticos dinámicos y relacionarla con propiedades energéticas
y disipativas evaluando
factores combinados de estas propiedades, y que mejor expliquen las
propiedades de las maderas acústicas, y que permitan la mejor selección de
maderas para la fabricación de fondos y aros de resonancia de cordófonos.
Schelleng (1963)
indica que la amortiguación de la radiación (Ar) dado por v/ρ, donde v la
velocidad del sonido relacionada con la energía elástica emitida y ρ la
densidad relacionada con la inercia de la madera cualidad vibracional, que es
similar para maderas con el mismo valor del factor (Ar), y que valores altos de
este factor, representan a maderas buenas emisoras de sonido. De otro lado, se
tiene la resistencia acústica (Ra) dada por vρ, que indica la
impedancia acústica de la madera. Yoshioka (2007) señala que la madera para
instrumentos musicales a cuerdas se divide princi-palmente en dos grupos de
maderas, para tapa acústica y para fondo y aro, propone clasificarlas
mediante la relación (v/δ), la velocidad dividida
entre el decaimiento logarítmico (δ), y compararla con el factor
(1/ρv) o inverso de la impedancia acústica; además, que la comparación
debe ser a frecuencias arriba de los 300 Hz para evitar la influencia de la
atenuación de las vibraciones. La comparación de estos parámetros permite identificar
las maderas de tapa con una correlación negativa entre los factores y madera de
fondo con alta correlación positiva de los factores. De otro lado, Obataya et al. (2000) recomiendan el estudio de la
matriz de las fibras y la porosidad celular a fin de caracterizar las
propiedades vibracionales de la madera y propone también, el uso del parámetro
v/δ para caracterizar la trasmisión por vibración de la madera; además
proponer el análisis de la ratio radial/longitudinal (δR/
δL) del decaimiento logarítmico en varias frecuencias de
resonancia para notar la anisotropía de la madera. Oktav (2024) señala la
influencia del espesor de la placa de resonancia del instrumento Karadeniz
kemenche, encontrando picos en 340 Hz y 900Hz para un espesor de 2,1mm y de 1040Hz
para el espesor de 1,7mm, en el presente estudio se fijará el estudio para
muestras de 3mm, de espesor evitando la influencia de la variación de este
parámetro en los resultados. Quintanilla et al. (2022) consideran que la
determinación descriptores para el estudio de maderas acústicas deben
contemplar la anisotropía y las propiedades ortotrópicas de la madera, Nop
& Tippner (2022), propone el uso de los estudios de los amortiguamientos
acústicos de la madera, para deter-minar los modos de vibración, su dirección
de propagación y frecuencia.
Mihălcică
et al. (2020) estudiando el comportamiento de guitarras con tapas de spruce (Picea
Abies L) y fondos de arce (Acer Pseudoplat) con pulsos en la zona
del puente muestran las respuestas de las tapas, que generan pulsos de casi 10
veces mayor, comparado con las del fondo; además de opacarse a frecuencias
mayores de 700 Hz. Mammoliti et al. (2024) señala la importancia de aprovechar
el uso de maderas consideradas de desechos industriales. Al proponer hacer evaluaciones
de las propiedades mecánicas antes de desecharlas, usando técnicas no
destructivas por sus bajos costos. Wong et al. (2025) indica la importancia de
evaluación de las propiedades mecánicas, de las maderas usadas en los
instrumentos musicales tradicionales y compararlas con las propiedades
mecánicas de muestras rectangulares de distintas especies. En este contexto el
objetivo de este estudio es encontrar la especie que mejor imita a una
tapa-acústica, usando el algoritmo MRMR de Machine Learning.
Las muestras
de madera estuvieron constituidas por trece especies, se incluyeron maderas de
uso tradicional nacionales, estas fueron: caoba (Swietenia macrophylla),
cedro (Cedrela odorata), estoraque (Myroxylon balsamum),
palisangre (Brosimun rubescens), diablo fuerte (Prumnopitys
harmsiana), nogal (Juglans sp.), especies exóticas nacionales como
ulcumano (Retrophyllum rospigliosii), dialium (Dialium guianense),
shihuahuaco (Dipteryx odorata), y palo azufre (Symphonia globulifera);
y especies importadas como: spruce (Picea engelmannii), palisandro (Dalbergia
latifolia), y arce (Acer saccharum); las últimas fueron sugeridas
por los lutieres y los dos primeros grupos fueron seleccionadas de una muestra
de 68 especies mediante técnicas aplicadas por los mismos, tales como el
percutir las maderas con los dedos percibiendo el sonido muy cerca al oído,
distinguir visualmente incluso al reflejo de la luz, palpar la dureza o rasgar
utilizando la uña, percibir el olor, sabor o lo agradable que sea a la vista.
Las muestras fueron provistas por la Empresa Industrial Amazónica Zapote
S.A–IMAZA. y fueron identificadas en la Facultad de Ciencias Forestales de la
Universidad Nacional Agraria La Molina (UNALM), Lima, Perú en el Laboratorio de
Propiedades Físico Mecánicas de la Madera, en el mismo fueron determinadas en
las propiedades de densidad y humedad de cada especie de acuerdo al
procedimiento estipulado en las Normas Técnicas Peruanas (NTP) 251.010 y la norma
NTP 251.011.
Las muestras
para la determinación de los parámetros acústicos tales como la velocidad
del sonido, la amortiguación de la radiación, la resistencia de onda acústica,
modos de vibración y el decaimiento logarítmico, fueron acondicionadas a
partir de piezas de madera según la orientación de sus fibras, diez probetas
radiales de 0,3 cm x 1,5 cm x 30 cm. y diez probetas longitudinales de 0,3 cm x
1,5 cm x 20 cm. por especie.
La velocidad
de transmisión del sonido se determinó con el Temporizador Ultrasónico, y
Microsecong timer (Fakopp, 2005), las mediciones se realizaron entre dos puntos
en sentido longitudinal y transversal a las fibras, manteniendo la relación
1/20 de las dimensiones entre el ancho/largo de las probetas. Se controló la
temperatura del entorno en 19 °C (±1 °C). y contenido de humedad promedio de
10,8 %.
Frecuencia de
resonancia experimentales
Los módulos de
vibración elástica
Se
determinaron valores para los tres primeros armónicos de acuerdo con las
posiciones de los apoyos para cada modo usando un percutor, micrófono (Shure) y
un osciloscopio, (Rohde & Schwarz), Figura 1.
Modos de vibración
y decaimiento logarítmico
Se efectuaron
pruebas iniciales recreando la forma como los luthieres percuten
la madera, con los nudillos de los dedos para oír el timbre de las resonancias.
Las cuales fueron determinadas, utilizando el programa analizador FFT de
frecuencias Fakopp, para determinar los modos de vibración: 1er, 2do o 3er armónico
en cada caso, Figura 1 y Figura 2, además, se visualizó la atenuación de la
onda de vibración a través de su decaimiento loga-rítmico. Se controló la
temperatura del entorno en 19 °C (±1 °C), con contenido de humedad promedio de
10,8%.
Decaimiento
logarítmico de la vibración
El decaimiento
logarítmico de la vibración (δ), relación 1, se determinó utilizando el
analizador de frecuencias Fakopp usando un analizador FFT de Fourier; para
tablillas tanto longitudinales como radiales. Sin embargo, Obataya et al.
(2000) indican que
en el caso radial podrían usarse pruebas de torsión,
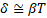 (1)
(1)
Donde β:
factor de decaimiento (1/s), β=C/2m; C es el coeficiente de rozamiento
viscoso (kg/s) y m es la masa de la muestra (kg); T: periodo (s).
En la Figura 2B se
muestra un proceso de medición simultaneo de dos espectros (FFT) usando la
misma APP, desfasados en tiempo lo que permite estimar el tiempo del
decaimiento, lo cual está relacionado al rozamiento interno en los procesos de
vibración interna de la madera.
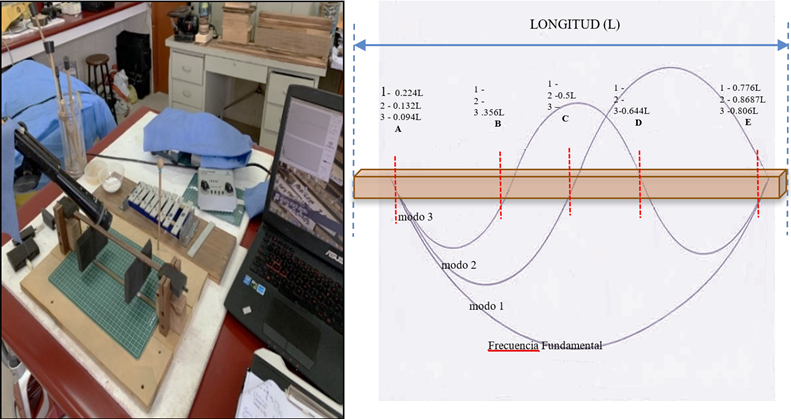
Figura 1. Modos de
vibración de una barra uniforme, los puntos A, B, C, D y E son los puntos de
los apoyos por cada modo.
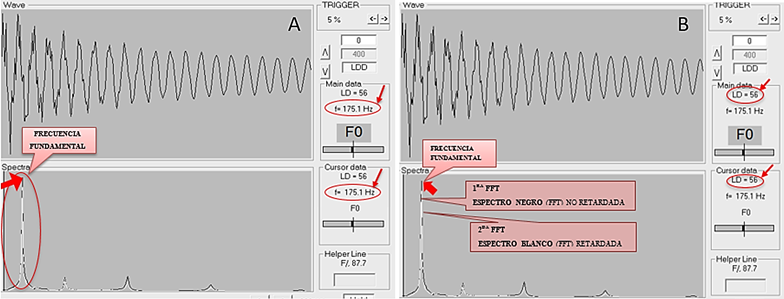
Figura 2. A. Ventana de
aplicación del analizador de frecuencias Fakopp indicando el valor de los modos
de vibración. y sus ubicaciones. B. Ventana del analizador indicando
los valores del decaimiento logarítmico y la ubicación de los espectros.
Cálculo del Amortiguamiento de la Radiación Sonora
La Amortiguación de Radiación Sonora
(Ar), se determinó mediante la
relación (2), (Kollmann & Côté,
1968), que relaciona la energía sonora
emitida con respecto a la energía total de la muestra de madera, los valores
actos indican maderas de tapa.
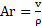 (2)
(2)
Donde Ar: Coeficiente de
la Amortiguación sonora, cm4/s. g; v: Velocidad del sonido (m/s) (Longitudinal
(L) o Radial; ρ: Densidad
corregida al 12 % (g/cm3).
Cálculo de la
resistencia acústica
La Resistencia de
la acústica (Ra), se determinó mediante la relación 3, (Kollmann & Côté,
1968). Indica la impedancia acústica de la madera y cuyos valores altos indican
maderas con buenas cualidades para el fondo de instrumentos musicales.
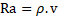 (3)
(3)
Donde Ra: Resistencia de
la onda acústica, g/cm2s.
Cálculo de
Parámetro de trasmisión (Pt)
Parámetro de
Trasmisión acústica (v/δ), se determinó a propuesta de Yoshioka S. (2007)
y Obataya et al. (2000), que relacionan el ratio:
de la velocidad del sonido y el decaimiento logarítmico (v/δ), que
caracteriza la conversión de la energía de trasmisión la vibración de la
madera, relación 4.
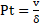 (4)
(4)
Donde Pt: Parámetro de
trasmisión acústica en cm/s; δ: Decaimiento logarítmico de la vibración.
Cálculo del factor
de Asimétrica radial/longitudinal del decaimiento logaritmo
Indica, la
asimetría energética radial longitudinal, propuesta por Obataya et al. (2000).
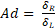 (5)
(5)
Donde δR: Decaimiento logarítmico radial; δL:
Decai-miento logarítmico longitudinal.
Densidad y
velocidad de propagación del sonido
Las densidades de
las especies presentaron valores entre 0,39 a 1,01 g/cm3 en un
intervalo de humedades de 9,4 a 12,4 %. En la Tabla 1 se presentan las
densidades corregidas al 12 % de contenido de humedad de las muestras, las
velocidades promedio de la propagación del sonido en sentido longitudinal y
radial, y las frecuencias de los modos de vibración longitudinales y radiales
de las muestras estudiadas.
Indicando, que se
encontraron valores mayores de las velocidades que las referencias revisadas,
debido posiblemente a las diferencias internas de las muestras así, para el
Spruce (Picea spruceanum) con 4790 m/s y para el cedro con 3770 m/s
(Kollmann & Côté, 1968).
Frecuencias de
resonancias longitudinales y radiales
Las
frecuencias experimentales, promedio para los modos del 1er, 2do
y 3er armónico en muestras longitudinales y radiales se presentan,
en la Tabla 1. Señalando que los valores obtenidos para las frecuencias
fundamentales de las especies como la caoba (Swietenia
macrophylla), el cedro (Cedrelela odorata) son más altos que los
encontrados por Sotomayor & Villaseñor (2018), para velocidades de 4682 m/s
y 4239 m/s, respectiva-mente.
Decaimiento
Logarítmico de la radiación
Con respecto
al Decaimiento logarítmico (δ), en la Tabla 2 se puede observar el
comportamiento del decaimiento logarítmico en el sentido longitudinal de varias
especies, sobresaliendo valores bajos en las especies caoba, palo azufre,
dalium y palisangre comparables con el spruce. Esto indica la calidad acústica
de estas maderas para la construcción de instrumentos musicales (Hatachan et
al., 2017), sobresaliendo el palisandro y diablo fuerte cuyos altos valores de
decaimiento logaritmo (especialmente en el 2do armónico) se debe posiblemente a
las características de fricción entre sus fibras, maderas que son usadas como
fondo en los instrumentos a cuerdas (Tabla 2 y Figura 3).
Tabla
1
Frecuencias
de resonancia experimentales promedio en muestras longitudinales y radiales para
las frecuencias del 1er, 2do y 3er armónico
|
Especie
|
Densidad
12 % g/cm3
|
Velocidad
(m/s)
|
Longitudinal
(Hz.)
|
Radial (Hz.)
|
|
Long.
|
Radial
|
1er
|
2do
|
3er
|
1er
|
2do
|
3er
|
|
Caoba (Swietenia macrophylla)
|
0,61
|
5326
|
1315
|
159,5
(10,3)
|
405,2
(19,0)
|
742
(66,2)
|
97
(3,0)
|
260
(5,0)
|
502
(14,9)
|
|
Cedro (Cedrela odorata)
|
0,47
|
5106
|
*
|
138
(14,3)
|
379,7
(32.6)
|
729,1
(57,1)
|
-
|
-
|
-
|
|
Diablo Fuerte (Prumnopitys armisiana)
|
0,67
|
5174
|
1194
|
131
(8,4)
|
355,5
(18,4)
|
680,5
(44,4)
|
87,1
(3,1)
|
231,4
(4,2)
|
451,9
(14,9)
|
|
Dialium (Dialium guianense.)
|
*
|
5661
|
*
|
165,3
(14,1)
|
449,4
(39)
|
865,2
(78)
|
-
|
-
|
-
|
|
Estoraque (Myroxylon balsamum)
|
0,87
|
4563
|
1951
|
146,5
(10,3)
|
406,5
(17,7)
|
772
(37,4)
|
144,3
(10,7)
|
384,2
(2,9)
|
746,3
(8,2)
|
|
Palisandro (Dalbergia latifolia)
|
0,56
|
5013
|
2018
|
172,3
(7,4)
|
461,3
(25,3)
|
872,7
(46,4)
|
167,6
(2,6)
|
443,1
(6,6)
|
845,4
(13,1)
|
|
Palisangre (Brosimun rubescens)
|
1,01
|
5100
|
1892
|
177
(7,7)
|
480,5
(28,4)
|
938,3
(56)
|
156,8
(10,9)
|
418,9
(30.3)
|
807,7
(58,3)
|
|
Palo Azufre (Symphonia globulifera)
|
0,71
|
5245
|
*
|
161,6
(6,6)
|
444,5
(12,6)
|
858,2
(23,2)
|
-
|
-
|
-
|
|
Shihuahuaco (Dipteryx odorata)
|
0,93
|
4824
|
2166
|
172,3
(12,8)
|
467.4
(33.3)
|
894
(62,6)
|
157,6
(12,7)
|
427,8
(26,9)
|
848,2
(32,4)
|
|
Spruce (Picea engelmanii).
|
0,39
|
5874
|
1694
|
189,2
(6,3)
|
513,9
(17,8)
|
998,4
(29,5)
|
136,1
(10,2)
|
350,1
(30,1)
|
658,5
(62,9)
|
|
Ulcumano (Retrophyllum rospigliosii)
|
0,44
|
4978
|
1116
|
157,9
(6,3)
|
433,2
(17,1)
|
840,7
(39,1)
|
208,1
(5,3)
|
400,1
(6,7)
|
654,5
(14,2)
|
Desviación
estándar (DS): entre paréntesis
Tabla
2
Decaimiento
logarítmico de la radiación en muestras longitudinales y radial para las
frecuencias del 1er, 2do y 3er armónico
|
Especie
|
Longitudinal
|
Radial
|
|
1er
|
2do
|
3er
|
1er
|
2do
|
3er
|
|
Caoba (Swietenia macrophylla)
|
0,0554
(0,014)
|
0,0594
(0,013)
|
0,0591
(0,073)
|
0,095
(0,024)
|
0,0960
(0,0291)
|
0,0977
(0.0176)
|
|
Cedro
(Cedrela odorata.)
|
0,0756
(0,017)
|
0,0578
(0,007)
|
0,0423
(0,093)
|
*
|
*
|
*
|
|
Diablo
Fuerte (Prumnopitys harmisiana)
|
0,1154
(0.031)
|
0,115
(0,030)
|
0,0523
(0,009)
|
0,1056
(0,029)
|
0,0960
(0,0256)
|
0,0577
(0.157)
|
|
Dialium
(Dialium guianense.)
|
0,0206
(0,004)
|
0,0339
(0,006)
|
0,0302
(0,0041)
|
*
|
*
|
*
|
|
Estoraque
(Myroxylon balsamum)
|
0,0617
(0,015)
|
0,0652
(0,008)
|
0,0384
(0,0035)
|
0,0637
(0,0164)
|
0,0524
(0,0164)
|
0,0547
(0,0154)
|
|
Palisandro
(Dalbergia latifolia)
|
0,0581
(0,017)
|
0,1030
(0,318)
|
0,060
(0,0175)
|
0,1350
(0,0335)
|
0,0850
(0,0175)
|
0,0421
(0,0075)
|
|
Palisangre
(Brosimun rubescens)
|
0,0197
(0,007)
|
0,0466
(0,0111)
|
0,0236
(0,007)
|
0,0728
(0,0161)
|
0,0674
(0,0161)
|
0,0486
(0,0066)
|
|
Palo
Azufre (Symphonia globulifera)
|
0,0347
(0,010)
|
0,052
(0,132)
|
0,0415
(0,0104)
|
*
|
*
|
*
|
|
Shihuahuaco
(Dipteryx odorata)
|
0,0460
(0,015)
|
0,0695
(0,0159)
|
0,0332
(0,006)
|
0,0559
(0,0152)
|
0,0592
(0,0173)
|
0,0540
(0,0154)
|
|
Spruce
(Picea engelmanii)
|
0,0496
(0,016)
|
0,0474
(0,0118)
|
0,0318
(0,005)
|
0,0411
(0,0411)
|
0,0688
(-)
|
0,0563
(0,011)
|
|
Ulcumano
(Retrophyllum rospigliosii)
|
0,0487
(0,016)
|
0,0660
(0,0111)
|
0,0410
(0,0116)
|
*
|
*
|
*
|
Desviación
estándar DS: entre paréntesis.
Pruebas
de la interacción del Amortiguamiento a la radiación con la Resistencia
acústica|
Los
valores promedios obtenidos de la relación entre (Ar) y (Ra) de madera en las
orientaciones longitudinal y radial se ilustran en la Tabla 3 y la Figura 4.
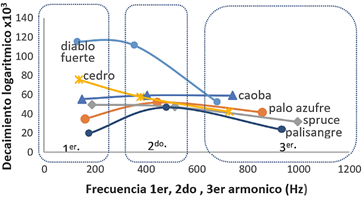
En
la Figura 4 se muestra el comportamiento en la dirección longitudinal, de la
relación Ar vs Ra, que permite diferenciar dos grupos en las maderas, los de
mayores valores de Ar que se ubican hacia la parte superior e izquierda y que a
su vez encierran a las maderas de bajas y medias densidades como el Spruce (Picea engelmanii, el Ulcumano (Retrophyllum rospigliosii), el Cedro (Cedrela
odorata) y la Caoba (Swietenia macrophylla); y el grupo de
mayores valores de Ra y menores Ar, que se ubican en la parte inferior derecha
y representan maderas de altas densidades, y están relacionadas con la
reflexión del sonido; se identificó este comportamiento en estoraque (Myroxylon
balsamum), shihuahuaco (Dipteryx odorata), palisangre (Brosimun
rubescens) y dialium (Dialium guianense) este último tanto en albura
y duramen.
Figura
3.
Decaimiento logarítmico (δ) en función de las frecuencias de resonancia
longitudinales (Hz) de la especie caoba, diablo fuerte, cedro, palo azufre,
palisangre y spruce.
Por otro lado, las
especies de densidades bajas tienen menos capacidad de conservar la energía
mecánica por lo que son importantes en la emisión
de energía, en el estudio se identificó este
comportamiento en spruce (Picea spruceanum), ulcumano (Retrophyllum rospigliosii), cedro (cedrela
odorata); y en las densidades medias pueden tener ambas funciones como con
el palisandro (Dalbergia latifolia), caoba (Swietenia macrophylla),
diablo fuerte (Prumnopitys harmisiana) y palo azufre
(Symphonia globulifera);
lo cual se confirma por lo expuesto por Schelleng (1968) y Yoshikawa (2007)
para clasificar las maderas con las mismas propiedades, comparando el factor
de Ar de las distintas maderas.
En secciones
radiales la relación de (Ar) y (Ra) en la Tabla 3, permiten también diferenciar
en las maderas estu-diadas dos grupos con tendencias similares mostradas para
la dirección longitudinal; sin embargo, los valores del Ar son del orden 3
veces menor por lo que energía emitida en la longitudinal.
Estos
comportamientos, están relaciones la calidad acústica a través de sus
características como, el efecto del tamaño de los anillos de crecimiento, y
debido posiblemente a la diferenciación entre zonas de duramen y albura. Esto
se puede visualizar en la ubicación de las muestras radiales de Spruce (Picea
spruceanum), de primera calidad y cuarta calidad (Tabla 3) donde se
comprobó que la diferencia entre la primera y cuarta calidad está relacionada
fuertemente con el ancho de los anillos de crecimiento encontrados al analizar
las muestras.
Figura 4. Relación entre la
amortiguación de la radiación del sonido (Ar =v/ρ) del sonido y la
resistencia de la onda acústica (Ra = ρv)
en muestras longitudinales (valores promedios).
Tabla 3
Valores de la
Amortiguación de la radiación (Ar). y la Resistencia acústica (Ra) en muestras
longitudinales (Long.) y radiales; usando unidades de102(cm4/g.
s) y 102(g/s.cm2) respectivamente
|
Especie
|
Amortiguación
Radiación
(Ar).
|
Resistencia
Acustica
(Ra)
|
Amortiguación
Radiación
(Ar).
|
Resistencia
Acustica
(Ra).
|
|
Long.
|
Long.
|
Radial
|
Radial
|
|
Caoba (Swietenia macrophylla)
|
9562,3
(507)
|
3237,3
(150)
|
2358,6
(86)
|
757,6
(42)
|
|
Cedro (Cedrela odorata)
|
11229,0
(531)
|
2429,0
(87)
|
*
|
*
|
|
Diablo
fuerte (Prumnopitys harmisiana)
|
8288,0
(396)
|
2785,2
(116)
|
2141,2
(45)
|
665,3
(19)
|
|
Dialium
(Dialium guianense), (duramen)
|
5631,2
(272)
|
5703,9
(100)
|
*
|
*
|
|
Estoraque
(Myroxylon balsamum)
|
5487,3
(183)
|
3796,2
(151)
|
2292,1
(80)
|
1620,3
(66)
|
|
Palisandro
(Dalbergia latifólia)
|
7814,4
(310)
|
3360,0
(172)
|
3141,9
(128)
|
1302,5
(48)
|
|
Palisangre
(Brosimun rubescens)
|
5251,8
(256)
|
4577,3
(247)
|
1994,5
(108)
|
1916,5
(83)
|
|
Palo szufre
(Symphonia globulifera)
|
8121,6
(439)
|
3389,0
(158)
|
*
|
*
|
|
Shihuahuaco
(Dipteryx odorata)
|
5460,7
(286)
|
4650,0
(235)
|
2299,5
(132)
|
1914,8
(97)
|
|
Spruce
(Picea engelmanii) (1ra)
|
15676,7
(858)
|
2260,8
(87)
|
4701,2
(229)
|
636,3
(32)
|
|
Spruce (Picea engelmanii)
(4ta)
|
*
|
*
|
3647,6
(155)
|
429,5
(11)
|
|
Ulcumano (Retrophyllum rospigliosii)
|
11172,1
(544)
|
2102,0
(102)
|
2658,0
(139)
|
464,1
(24)
|
Desviación estándar
DS: entre paréntesis.
Pruebas de la
interacción del decaimiento logarít-mico de la radiación
Relación entre el
Paramero de trasmisión (Pt=v/δ) y el Inverso de la Amortiguación de la
radiación
(1/Ar = ρ/v).
De
otro lado, de acuerdo con lo propuesto por Yoshioka (2007), que relaciona el
Parámetro de trasmisión (Pt = v/δ), y el Inverso de la Amortiguación de la
radiación (1/Ar =ρ/v) (Figura 5) y usando los valores 2do
armónico del decaimiento logarítmico y la madera de caoba como referencia para
trazar las dos líneas ortogonales referenciales, que mostrar las zonas de
madera de tapa acústica en el lado izquierdo y maderas para el fondo acústico
en el lado derecho del gráfico.
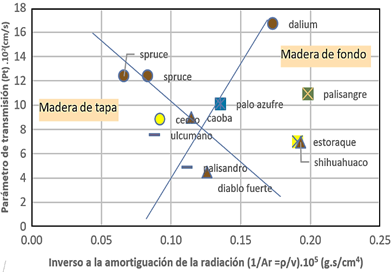
Figura 5. Gráfico
entre el Paramero de trasmisión (Pt=v/δ) vs (1/Ar =ρ/v); considerando
la caoba como la madera de referencia para dividir los cuadrantes de madera
de fondo y madera de tapa.
Se muestra
claramente las dos maderas spruce y el cedro como maderas de tapa acústica y
las maderas de estoraque, shihuahuaco, palo azufre, palisandro y dalium como
los más recomendables como madera de fondo acústico; lo que muestra la
importancia del uso del factor Pt en la evaluación de maderas acústicas.
Relación entre
el factor de Asimétrica del decai-miento logarítmico Ad = δR/δL, vs la densidad
de las distintas maderas estudiadas
En la Figura 6
se muestra el factor de Asimetría del decaimiento logarítmico (Ad= δR/δL), para el tercer
y el
primer
armónico de las maderas estudiadas vs su densidad; se observa claramente el comportamiento
del spruce y la caoba que no casi no cambian sus valores, en comparación de las
otras maderas que muestran la variación del factor y señalando la posible
anisotropía de su estructura interna, y mostrando las buenas cualidades
acústicas de las primeras. Esto servirá para evaluar mejor las maderas
acústicas para la construcción de instru-mentos musicales.
Shirmohammadi et al. (2020), estudiando las cualidades
mecánicas y fricción interna de 15 maderas australianas, encontrar cuatro
maderas con potencial de uso en la fabricación de diapasones, recomendando
efectuar la evaluación acústica y anatómica de las maderas estudiadas, usando
las técnicas no destructivas.
En las Tablas
3 y 4 se muestra el consolidado de los factores que permiten caracterizar las
propiedades acústicas de las maderas estudiadas en el segundo armónico para Pt
y Ad, sobresaliendo los altos valores de Ar y Ra de las maderas de la caoba y
spruce. Maderas de alto valor de Ar y valores bajos de Ra, como spruce, cedro y
ulcumano, son buenos emisores de energía. Las maderas como dalium, shihuahuaco
y palisangre, con bajos valores de Ar y altos valores de Ar, son buenos
emisores de energía (Figura 4). También se muestra con valores medios de Ar y
Ra a la caoba, diablo fuerte, palisandro y palo azufre. Por lo que, las
cualidades sonoras de los instrumentos pueden ser analizadas por las técnicas
acústicas utilizadas en el estudio.
De otro lado,
en la dirección radial se muestra un comportamiento similar, sin embargo, los
valores de Ar y Ra son mucho menores de ambos parámetros.
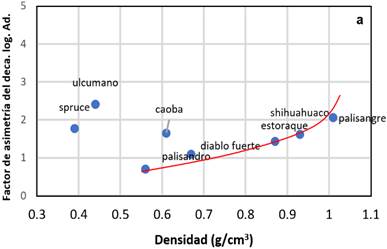
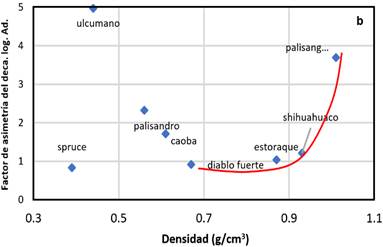
Figura 6. Relación
factor Asimetría del decaimiento logarítmico (Ad =
δR /δL) vs densidad (ρ=g/cm3),
para el tercer (a) y primer armónico (b).
En la Tabla 4 se puede ver como los factores estudiados
pueden servir para caracterizar las maderas acústicas, lo cual permite decidir,
sobre el mejor el uso acústico de las diferentes especies de madera. Lacardi et al.
(2022), usando modelos de metamateriales estudian maderas efectuando
perforaciones en las tapas y evaluando las modificaciones en las propiedades
modales del instru-mento, proporcionando una nueva forma de probar nuevos
materiales acústicos.
Stanciu (2022), evalúa
dinámicamente los cambios acústicos de la madera y propone cuatro etapas de
fabricación de guitarras y de evaluar los patrones de Chladni a diferentes
frecuencias de vibración, indicando que las nuevas técnicas permitirán un
avance significativo en la fabricación de instrumentos musicales. Además, Viala
et al. (2020) recomiendan la calificación de la calidad en la adquisición de
las maderas, efectuar las pruebas acústicas tanto en la madera como en los
instrumentos ya acabados.
Bucur (2023) señala
la importancia de las pruebas no destructivas en la evaluación de maderas
acústicas, en especial las diferencias acústicas que causan el uso de maderas
de diferentes especies al utilizarlo en la fabricación de instrumentos
musicales.
Finalmente,
Carcagno et al. (2018) en estudio de la influencia del fondo de guitarras con 6
maderas como palo rosa, caoba, sapeli, arce y nogal y otras en un total de 52
guitarras a cuerdas metálicas, indican que la diferen-cia de las maderas de
calidad solo tuvo impacto marginal al sonido percibido al efectuarse pruebas de
evaluación por un panel al ejecutarse los instrumentos, lo que indica la
necesidad de seguir haciendo estudios de caracteri-zación acústicas de estas
maderas.
Tabla 4
Consolidado de
las propiedades de las maderas con respecto a los factores estudiados
|
Madera
|
Ar
|
Ra
|
Pt
|
Ad
|
|
caoba
|
β
|
β
|
β
|
α
|
|
spruce
|
α
|
γ
|
β
|
α
|
|
cedro
|
β
|
γ
|
β
|
*
|
|
palisandro
|
γ
|
β
|
γ
|
γ
|
|
ulcumano
|
β
|
γ
|
γ
|
*
|
|
Palo azufre
|
γ
|
β
|
β
|
*
|
|
Shihuahuaco
|
γ
|
α
|
γ
|
γ
|
|
dalium
|
γ
|
α
|
α
|
*
|
|
estoraque
|
γ
|
β
|
γ
|
γ
|
|
palisangre
|
γ
|
α
|
β
|
α
|
Α: alto,
β: medio y γ: bajo. Representan los valores encontrados de estos
factores.
Las
maderas de
palisangre (Brosimun rubescens),
palo azufre
(Symphonia globulifera), estoraque (Myroxylon balsamum),
shihuahuaco (Dipteryx odorata), y dialium (Dialium guianense) presentan
propiedades acústicas con aptitud para la fabricación de
fondos y aros de resonancia en cordófonos; en especial las maderas de palisangre y palo
azufre, que fueron recomendadas por luthieres.
Los factores como,
amortiguación a la radiación (Ar), resistencia acústica (Ra), parámetro de
trasmisión (Pt) y Asimetría del decaimiento logarítmico radial/ longi-tudinal (Ad), son buenos indicadores de maderas acústica.
El uso de técnicas
acústicas no destructivas, permiten una evaluación optima de las propiedades
acústicas de las maderas, reduciendo los costos y aumentando la rapidez de las
mediciones
La divulgación de
estas técnicas acústicas no destructivas podría ayudar al desarrollo de la industria
de instrumentales en el Perú, y potenciar el uso de maderas tropicales con
propiedades acústicas.
Se propone el uso
de algoritmos como Machine Learning para utilizar las propiedades acústicas las
maderas tradicionales como el spruce, palisandro y caoba comparándolas con las
nuevas maderas encontradas.
REFERENCIAS
BIBLIOGRÁFICAS
Bucur, V. (2023). A Review on Acoustics of
Wood as a Tool for Quality Assessment. Forests, 14(8), 1545.
Carcagno, S., Backnall, R., Woodhouse, J., Frirz, C., & Plack
C. (2018). Effect of back wood choice on the perceived quality of steel-string
acoustic guitars. J.
Acoust. Soc. Am. 144, 3533–3547.
De la Cruz, R., Carrillo,
A., Nájera, J., Cruz, F., Javier, F., & Méndez, J. (2018). Durabilidad
natural de siete especies forestales de El Salto, Durango. Revista Mexicana de
Ciencias Forestales, 9(46). https://doi.org/10.29298/rmcf.v9i46.144
Fakopp Enterprise Bt- C.
(2005). FAKOPP Ultrasonic Timer y Microsecong-timer User’s Guide. Fakopp Enterprise
publication. HU.
Halachan, P., Babiak, M.,
Spisiak, D., Chuinsky, A., Tambi, A., & Chauzov, K. (2017). Physic acoustic
characteristics of spruce and larche wood. Wood Research, 62(2), 235-242.
Kollmann, F.P. y Côté W.A.
(1968). Principles of Wood Science and Technology: Solid Wood. München, (v.1,
.274 – 285). Alemania, Springer – Verlag Berlin Heidelberg New York.
Lercari,
M., Gonzalez, S., Espinoza, C., Longo, G., Antonacci, F., & Sarti, A.
(2022). Using mechanical metamaterials in guitar top plates: a numerical study.
Applied Sciences, 12(17), 8619.
Mihălcică, M., Stanciu, M., & Vlase, S. (2020). Frequency
response evaluation of guitar bodies with different bracing systems. Department
of Mechanical Engineering, Transilvania University of Bras, Symmetry.
Mammoliti, A., Cataldo, M., Papandrea, S., & Proto A.
(2024). Machnical propierties of Branch and stem wood for two Mediterranean
cultivars of olive tree. Journal of Wood Science, 70, Art. 40. https://doi.org/10.1186/s10086-024-02153-1
Normas Técnicas Peruanas (NTP). 2004. "Maderas. Método de
Determinación de Contenido de Humedad". Norma Técnica Peruana 251.010. 2da
edición. Comisión de Reglamentos Técnicos y Comerciales - INDECOPI.
Lima, Perú. 7p.
Normas
Técnicas Peruanas (NTP). 1980. "Maderas. Método de Determinación de
Densidad". Norma Técnica Peruana 251.011. 2da edición. Comisión
de Reglamentos Técnicos y Comerciales - INDECOPI. Lima, Perú. 7p.
Nop P., & Tippner J.
(2022) Influencia de las dimensiones de muestras de madera para la
determinación de parámetros acústicos y timbre sonoro. Acústica
Aplicada,
196, 108895.
Obataya, E., Ono, T., &
Morimoto, M. (2000). Vibrational properties of wood along the grain. Journal
of Materials Science, 35, 2993-3001. https://doi.org/10.1023/A:1004782827844
Okyav A. (2024). The
variation in the acoustic response of the Karadeniz Kemenche depending on the
thickness of the soundboard. Acustic Australia. https://doi.org/10.1007/s40857-024-00345-9
Quintavalla, M., Gabrielli,
F., & Canevari, C. (2022). Grading materials for stringed instruments
soundboards: An approach considering the orthotropic elastic and damping
properties. Applied Acoustics, 187, 108521. https://doi.org/10.1016/j.apacoust.2021.108521
Schelleng, J. (1963). The
violin as a circuit. J. Acoust. Soc. Am., 35, 326–338.
Shirmohammadi,
M., Faircloth, A., & Redman, A. (2020). Deter-mining
acoustic and mechanical properties of Australian native hardwood species for
guitar fretboard production. European Journal of Wood and Wood Products, 78,
1161-1171. https://doi.org/10.1007/s00107-020-01599-6
Sotomayor, J., & Villaseñor, J. (2018). Propiedades
materiales e índices de rendimiento acústico de veintidós maderas mexicanas,
determinación por ultrasonido. Madera y Bosque,
24(3), e2431132 https://doi.org/10.21829/myb.2018.2431132
Stanciu,
M. D., Rosca, I. C., Mihălcică, M., & Bucur, V. (2022). Dynamic
response of wooden plates in different stages of guitar manufacturing. European
Journal of Wood and Wood Products, 80(4), 997-1013. https://doi.org/10.1007/s00107-022-01817-3
Viala, R., Placet, V., & Cogan, S.
(2020). Simultaneous non-destructive identification of multiple elastic and
damping properties of spruce tonewood to improve grading. Journal of
Cultural Heritage, 42, 108-116. https://doi.org/10.1016/j.culher.2019.09.004
Wong. T., Soong. M., Saifizul. A., &
Ramli. (2025). Assessment of quality for Sape making: vibroacoustic analysis
and machine learning classification. Expert Systems with Applications, 261,
125591. https://doi.org/10.1016/j.eswa.2024.125591
Yoshioka, S. (2007). Acoustical classification of woods for
string instruments. Journal of Acoustic Society of America, 122(1),
568-573. https://doi.org/10.1121/1.2743162