 |
INTRODUCCIÓN
Aplicación de hidrogramas unitarios mediante el producto PISCO (Peruvian Interpolated data of SENAMHI's Climatological and Hydrological Observations) para la generación de caudales máximos
Application of unit hydrographs using the PISCO product (Peruvian Interpolated data of SENAMHI's Climatological and Hydrological Observations) for the generation of maximum flows
Jairo Isaí Alvarez Villanueva1; José Francisco Huamán Vidaurre1
* Autor corresponsal: jialvarezv@unc.edu.pe (J. I. Alvarez Villanueva).
ORCID de los autores:
J. I. Alvarez Villanueva*, https://orcid.org/0000-0001-8777-3943 J. F. Huamán Vidaurre, https://orcid.org/0000-0002-4896-0479
RESUMEN
El objetivo fue aplicar Hidrogramas Unitarios mediante el producto PISCO (Peruvian Interpolated data of SENAMHI's Climatological and Hydrological Observations) para la generación de caudales máximos. Se contó con información de caudales mensuales máximos de la estación hidrométrica “Yonán” del río Jequetepeque, con la precipitación máxima mensual de 8 estaciones terrestres de la cuenca alta del “Jequetepeque” y precipitaciones máximas mensuales de data grillada espacial de lluvia mencionada anteriormente para el período 1981-2019. Se utilizó el modelo HU Triangular de la SCS y HU Sintético de Snyder. El tiempo de concentración para el área de cuenca (3294,68 km2) es de 8,61 horas, y el número de curva es 77,65. La variabilidad entre las precipitaciones máximas mensuales de la data grillada espacial de lluvia mencionada y 8 estaciones terrestres de la cuenca alta, fue baja en siete estaciones meteorológicas (0,68 < R2 <0,79) y alta en 1 estación (R2 = 0,37). Los caudales máximos anuales generados por lo modelo indicados mostraron una sobre estimación con respecto a los caudales máximos observados para diferentes tiempos de retorno. Se agrego un exponente al modelo del HU Triangular de la SCS para aproximar a los caudales máximos anuales próximos a los caudales máximos anuales de la estación “Yonán” para diferentes tiempos de retorno. Esto generó un buen ajuste, según la métrica de los estadísticos del Coeficiente de determinación (0,99) y Nash (0,98).
Palabras clave: data grillada; data espacial de lluvia; caudal máximo; río Jequetepeque.
ABSTRACT
The objective was to apply Unit Hydrographs using the PISCO product (Peruvian Interpolated data of SENAMHI's Climatological and Hydrological Observations) for the generation of maximum flows. Information was available on maximum monthly flows from the "Yonán" hydrometric station on the Jequetepeque River, with maximum monthly precipitation from 8 terrestrial stations in the upper Jequetepeque basin and maximum monthly precipitation from previously mentioned gridded spatial rainfall data for the period 1981-2019. The SCS Triangular Unit Hydrograph model and Snyder Synthetic Unit Hydrograph were used. The concentration time for the watershed area (3294.68 km²) is 8.61 hours, and the curve number is 77.65. The variability between the maximum monthly precipitation from the mentioned gridded rainfall data and 8 ground stations in the upper basin was low in seven meteorological stations (0.68 < R2< 0.79) and high in 1 station (R2 = 0.37). The maximum annual flows generated by the indicated model showed an overestimation compared to the observed maximum flows for different return periods. An exponent was added to the SCS Triangular HU model to approximate the annual maximum flows close to the annual maximum flows of the "Yonán" station for different return periods. This generated a good fit, according to the metrics of the determination coefficient (0.99) and Nash (0.98) statistics.
Keywords: gridded data; spatial rainfall data; maximum flow; Jequetepeque River.
Recibido: 18-11-2024.
Aceptado: 02-03-2025.
Para el diseño de obras hidráulicas, el principal problema es la falta de información pluviométrica para estimar el caudal de diseño (Alejo et al., 2022). El caudal máximo anual es una variable hidrológica influenciada por la morfometría de la cuenca, la red de drenaje y características climáticas, útil para la gestión de eventos extremos de crecidas Para estimar caudales máximos con bajo grado de incertidumbre es preciso contar con una amplia información hidrometereológica (Méndez et al., 2015; Lauro et al., 2021). Las series de caudales máximos anuales de ríos obtenidos mediante aforos no siempre están disponibles en muchas cuencas, esto dificulta utilizar métodos estadísticos basados en funciones de distribución de variable aleatoria, útiles para determinar el caudal máximo (Chen & Singh, 2017). Al no poder calcular el caudal de avenida máxima mediante métodos estadísticos, debido a la falta de series de caudales máximos, se utilizan métodos alternativos, como son los modelos de lluvia - escorrentía (Młyński et al., 2019). Los caudales máximos, están relacionados a tormentas de diferente tiempo de retorno (Castillo García & Carvajal González, 2023) .En ríos donde no se cuenta estaciones de aforo para estimar el caudal máximo, se recurre a modelos hidrológicos. Esta estimación de caudales está propenso a presentar incertidumbre, si no se cuenta con datos de aforo observados (Skidelsky et al., 2023). En la práctica los hidrólogos utilizan hidrogramas unitarios sintéticos tales como: Snyder, SCS-UH, Clark-UH entre otros, para transformar la lluvia a escorrentía. Mediante una serie hidrológica de precipitación pluvial, es posible predecir la precipitación no observada, para esto se utiliza funciones de distribución de probabilidad de variables aleatorias para diferentes tiempos de retorno. Las funciones de distribución de probabilidad más comunes son: distribución Normal, Distribución Logarítmica normal, Tipo III de Pearson, Función Exponencial, Distribución de Gumbel, Distribución Generalizada de Valores Extremos (GEV) y Distribuciones de Weibull y Pareto (Boudrissa et al., 2017; Douka et al., 2017). La selección de una función de distribución de frecuencia permite estimar la magnitud de un evento útil en el diseño de infraestructura hidráulica, relacionado al drenaje urbano, represas, aliviaderos, diques, alcantarillas, drenaje de carreteras entre otros (Beven & Hornberger, 1982). El análisis de frecuencia de lluvia para inundaciones comúnmente utiliza las funciones de distribuciones de probabilidad, tales como: Gumbel, Gamma, valor extremo generalizado (GEV), Pearson tipo III (P-III), log-Pearson tipo III (LP-III), Weibull y Log-normal (LN). Algunos países han adoptado funciones de distribución para estudios de inundaciones, tales como: China y Australia quienes adoptaron la función de distribución (P-III), como una metodología estándar para el estudio hidrológico. Por otro lado, Estados Unidos adoptó la distribución LP-III, mientras que en Europa la distribución GEV (Shao et al., 2004; Chen et al., 2010; Guo et al., 2012). El mundo mediante el cambio climático está experimentado cambios en el régimen hidrológico y distribución espacial de las lluvias, esto genera que la predicción de la precipitación pluvial sea cada vez más difícil (Tye & Cooley, 2015). Comprender las características hidrológicas de una región es importante, para comprender sus problemas y así dar soluciones en la gestión del recurso hídrico (Sousa Rocha et al., 2021). La data PISCO es una información grillada de precipitación perteneciente a la institución peruana SENAMHI, cuya capacidad permite generar caudales máximos en un cauce principal (Carmona Arteaga et al., 2021). Los datos espaciales PISCO, son un producto satelital de lluvias. Las siglas del producto PISCO, significan: Peruvian Interpolated data of the SENAMHI's Climatological and Hydrological Observations. Esta data espacial de lluvia permite cubrir vacíos de información pluviométrica del territorio peruano. La data de PISCO v2.1, actualmente, se encuentra en versión diaria y mensual a nivel nacional. La data tiene una serie temporal comprendido entre el 1 enero de 1981 hasta el 1 de diciembre de 2016, en el portal de la Autoridad Nacional del Agua (Aybar et al., 2017). Los datos PISCO, son datos espaciales de lluvia, cuya base de datos corresponde al proyecto CHIRP, los cuales cubren vacíos de información pluviométrica y permite entender el proceso dinámico espacial de la lluvia dentro de una cuenca (Ticse De la Torre & Moya Álvarez, 2019). De los productos grillados, es posible extraer precipitación máxima anual histórica, para generar caudales asociados a diferentes tiempos de retorno (Videla Valdebenito, 2023). Los datos de precipitación obtenidos de imágenes de satélite se encuentran distribuidos en el espacio de manera uniformemente. Esta información es una alternativa para la modelación hidrológica (Espinosa-López et al., 2024). Finalmente, el objetivo de la investigación fue aplicar hidrogramas unitarios mediante el producto PISCO (Peruvian Interpolated data of SENAMHI's Climatological and Hydrological Observations) para la generación de caudales máximos.
METODOLOGÍA
Zona de estudio
El área de estudio de la cuenca alta del Jequete-peque (Figura 1) es de 3288,8 km2, ubicada en el Distrito de “Yonán”, provincia de Cajamarca, Departamento y Región de Cajamarca. La estación “Yonán” del río “Jequetepeque”, se encuentra ubicada en la zona media de la mencionada cuenca, aguas arriba de la presa Gallito Ciego. Sus coordenadas son Lat. 07° 15’ 21.30” S y Long. 79° 05’ 56.70” a una altitud de 457 msnm. Además, la circulación y distribución de las aguas superficiales de la red de drenaje de la cuenca alta del “Jequetepeque” pertenecen a la vertiente del Pacífico.
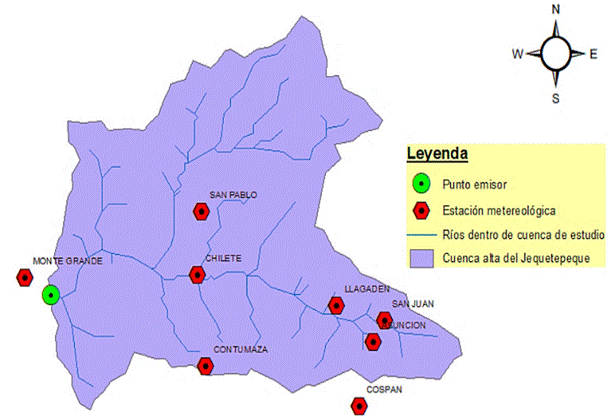
Figura 1. Estaciones meteorológicas dentro de la cuenca alta de Jequetepeque.
Información histórica de caudales de río Jeque-tepeque
Se consideró una serie hidrológica de caudales mensuales del período 1981-2016 del río “Jeque-tepeque”. Los mencionados caudales fueron regis-trados por la estación hidrométrica Yonán, propor-cionados por el Proyecto Especial Jequetepeque Zaña (PEJEZA). Asimismo, la precipitación espacial mensual de lluvia se obtuvo de la data grillada de precipitación de SENAMHI que cubre el período 1981-2016. Las precitaciones observadas a escala mensual de 8 estaciones meteorológicas conven-cionales se obtuvieron de Rivasplata (2019).
Modelos determinísticos para determinación el tiempo de concentración
Vélez et al. (2013) indican que para observar el tiempo de respuesta de la cuenca hidrográfica es necesario contar con varios métodos determinísticos, siendo apropiado contar con por lo menos cinco estimaciones. Según Upegui & Gutiérrez (2011), señalan que el tiempo de concentración se estima mediante un valor medio de metodologías establecidas (Tabla A1), con el fin de separar los valores distanciados de la media. Para luego calcular la media de los restantes.
El tiempo de concentración (tc) (h) se obtuvo de las fórmulas presentadas en la Tabla 1. Los modelos empíricos indicados necesitaron información de parámetros morfológicos, tales como: la longitud del cauce principal (L) (km), el cual fue considerado hasta el límite de la divisoria de agua de la cuenca, la pendiente media de la cuenca (S) (m/m) obtenido de la diferencia de alturas (m) entre la longitud del cauce principal, S0 es la pendiente expresada en porcentaje y el área de la cuenca (A) (km2).
Número de curva y coeficiente de escorrentía
En los últimos años los modelos hidrológicos están cumpliendo un papel fundamental en la repre-sentación de distribución de lluvias y la estimación de caudales. Mediante el uso de mapas temáticos y el modelo empírico del Número de Curva del Servicio de Conservación de Suelo (SCS), es posible estimar la infiltración. Este valor será fundamental para estimar la escorrentía superficial (Portuguez & Verano, 2016).
La investigación utilizó diversos mapas de cober-tura vegetal de condiciones húmedas y secas, textura de suelos, grupos hidrológicos, modelos digitales de elevaciones (MDE) y un Sistema de Información Geográfica (SIG), para estimar el Número de Curva. Se tomó en cuenta el manual de Generación de Mapa Temático de Curva de Número dados por la Autoridad Nacional de Agua, para clasificar al grupo hidrológico de la cuenca, cuyos grupos hidrológicos fueron B y C. Además, para determinar el número de curva de la zona de estudio, se utilizó la Fórmula 1.
![]() (1)
(1)
Comparación de precipitaciones mensuales de las estaciones meteorológica terrestre con la
información grillada de precipitación de base de datos PISCO del SENAMH
Es importante tener en cuenta que, para el ajuste de una función de distribución probabilística, se utiliza un nivel de significancia del 5%. Se utilizó el indicador estadístico del coeficiente de correlación y Nash como métricas de bondad de ajuste. Se utilizó el programa R Estudio Cloud, para establecer la variación entre las precipitaciones máximas mensuales del producto PISCO (Peruvian Interpolated data of SENAMHI's Climatological and Hydrological Observations, obtenida del enlace https://iridl.ldeo.columbia.edu/SOURCES/.SENAMHI/.HSR/.PISCO/), y las precipitaciones máximas men-suales de 8 estaciones terrestres meteorológicas convencionales (Figura 1).
Precipitaciones mensuales máxima para dife-rentes tiempos de retorno
Antes de generar precipitaciones para diferente tiempo de retorno, la información de precipi-taciones máximas mensuales pasó por un proceso de análisis de datos dudosos (Outlier). Se utilizó distribuciones teóricas probabilísticas, tales como: Normal, LogNormal 2 parámetros, LogNormal 2 parámetros, Gamma 2 parámetros, Gamma 3 parámetros, LogPearson tipo III, Gumbel y LogGumbel, para un nivel de significancia del 5%. Y para realizar el ajuste de los datos de la serie hidrológica de precipitaciones máximas mensua-les, se usó la prueba de Kolmogórov-Smirnov. Se utilizó el programa Hidroesta2 para el análisis estadístico.
Precipitación efectiva
Según Villazón Gómez et al. (2021) la precipitación efectiva es parte de una tormenta neta de caída sobre una superficie. Asimismo, Espinales Cedeño et al. (2021) señalan que esta información permite estimar la escorrentía directa (Tabla 1).
Cálculo de caudal máximo anual mediante hidrogramas unitarios
En la ingeniería hidrológica, la fase de planificación y diseño de estructuras hidráulicas, el hidrograma unitario (HU) es el método más utilizado (Ayuso et al., 1994). Los HU son herramientas para la estimación de caudales máximos en cuencas hidrográficas que no cuenten registros históricos de mediciones de caudales máximos (Pedroso & Mannich, 2021).
a) Hidrograma Unitario Triangular (HUT) de la SCS: la Tabla A5 presenta los componentes necesarios para calcular el caudal máximo mediante el Hidrograma Unitario Triangular de la SCS (Da Silveira, 2016; Carmona et al., 2021).
b) Hidrograma Unitario Sintético (HUS) de Snyder: la Tabla A6 presenta los componentes necesarios para calcular el caudal máximo mediante el Hidrograma Unitario Sintético de Snyder.
Tabla 1
Expresiones para estimar la precipitación efectiva
|
Descripción |
Unidad |
Expresión |
Componentes |
N° |
|
Factor de retención |
(mm) |
|
NC: Número de curva |
2 |
|
Precipitación efectiva |
(mm) |
|
P: Lamina de lluvia neta S: Factor de retención |
3 |
Fuente: (Da Costa et al., 2019; Espinales Cedeño et al., 2021; Carmona et al., 2021).
RESULTADOS Y DISCUSIÓN
Mediante un modelo digital de elevación obtenido de Alos Palsar de resolución de 12,5 m https://asf.alaska.edu/datasets/daac/alos-palsar/
correspondiente a la zona UTM 17S, de estudio mencionado y el uso de un sistema de información geográfica (SIG), se obtuvo la información presentada en la Tabla 2 y Figura 2. La información de la Tabla 2 permitió estimar el tiempo de concentración (Tabla A1). Según Portuguez & Verano (2016), para generar mapas temáticos de número de curva (NC) para la cuenca de estudio, se utilizó las herramientas del Sistema de Información Geográfica (GIS). Asimismo, se estableció para la cuenca alta del Jequetepeque un valor de número de curva de 77,65 (Figura 2 y Fórmula 1).
Se utilizó SIG y la metodología de Enrique Blair (1963) para calcular el coeficiente de escorrentía, cuyo valor resultó en 0,65 (Tabla 2). La Tabla A1 muestra la estimación del tiempo de concentración para la cuenca alta del Jequetepeque, a partir de 11 métodos determinísticos y resultó igual a 8,61 horas. La Figura 3 presenta caudales máximos anuales del período 1981-2016. El caudal máximo fue de 305,68 m3/s y el menor fue de 20,95 m3/s. El río Jequetepeque tiene una escorrentía perenne y que la zona de estudio presenta periodos con bajas considerables de caudal. La duración de estiaje es más prolongada y los caudales máximos tiene una tendencia a aumentar (Figura 3).
Tabla 2
Parámetros físicos y complementarios para la cuenca en estudio
|
Parámetros |
Valor /Característica |
|
|
Punto de control (PC) |
Estación hidrométrica Yonán |
Unidad |
|
Área de drenaje (A) |
3294,68 |
km2 |
|
Pendiente de cauce principal (S) |
13,93 |
% |
|
Pendiente de cauce principal (S0) (en tanto por uno) |
0,0383 |
m/m |
|
Longitud de cauce principal (L) |
95,94 |
km |
|
Cota máxima de longitud de cauce (H máx) |
4146,33 |
msnm |
|
Cota mínima de longitud de cauce (H min) |
469,37 |
msnm |
|
Coeficiente de escorrentía (C) |
0,65 |
- |
|
Numero de curva (NC) |
77,65 |
- |
|
Distancia entre la salida y el centro de gravedad de la cuenca (LCG) |
36.76 |
km |
|
|
|
|
|
|
Figura 2. Mapa temático para estimar el número de curva y coeficiente de escorrentía.
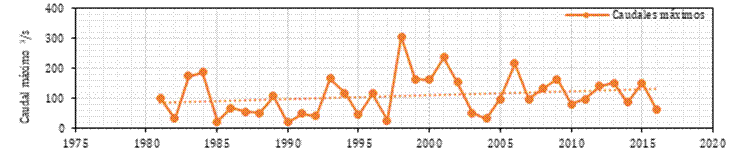
Figura 3. Caudal máximo obtenido de la data de caudales mensuales de la estación hidrométrica Yonán, 1981-2016.
Fuente: PEJEZA (2021).
Se descargó las precipitaciones mensuales del período 1981-2016 de la cuenca alta del Jequetepeque de un área igual 3288.8 km2, del producto PISCO (Peruvian Interpolated data of SENAMHI's Climatological and Hydrological Observations) de la Autoridad Nacional del Agua del portal https://snirh.ana.gob.pe/ANDREA/. Posteriormente se seleccionó los valores máximos de la lámina de lluvia (mm), ver Figura 4. Estos valores fueron analizados a partir del método de datos dudosos, la información resultante se presenta en la Figura 4. Se observa una tendencia a aumento en la lámina de la lluvia. Posteriormente, esta información sirvió para determinar láminas de lluvia para diferente tiempo de retorno, a través de funciones de distribución de probabilidad.
La Tabla A2 muestra la comparación estadística entre las precipitaciones máximas mensuales de la data grillada espacial de lluvia llamada PISCO (Peruvian Interpolated data of SENAMHI's Climatological and Hydrological Observations), con respecto a las precipitaciones máximas mensuales de 8 estaciones meteorológicas terrestres convencionales a escala mensual, tomado de Rivasplata (2019). Las estaciones indicadas corresponden a estaciones dentro de la cuenca alta del Jequetepeque (Figura 1). La Tabla A2 muestra valores métricos obtenidos a partir del estadístico de coeficiente de determinación. Siete de las estaciones, corresponden a un rango comprendido entre 0,68 y 0,79 próximos a 1. Mientras que estación estación Llagaden, obtuvo un valor de determinación de 0,37, tal como se describe en la Tabla A2 Para obtener la información de la Tabla 3, se utilizó la información de la Figura 4.
La Tabla 3 presenta precitaciones máximas para diferente tiempo de retorno, generados a partir de la función probabilístico Gama 3 parámetros, esta función se seleccionó mediante la prueba de bondad de ajuste de Kolmogorov-Smirnov. A los valores de la precipitación obtenidos para diferente tiempo de retorno de la Tabla 3, se le multiplicó por un factor de 1,13 (Campos, 1998) señala que Weiss propuso un factor de corrección con la finalidad de compensar la subestimación de lluvias máximas diarias que cae en intervalos de 24 horas. Y llama a este método como corrección por intervalo fijo de observación.
Para obtener la precipitación efectiva para el modelo HUT de la SCS se utilizó la Tabla 1, Tabla 2, Tabla 3, Figura 2 y Tabla A3. Por otro lado, para obtener la precipitación efectiva para el HUS de Snyder se utilizó la Tabla 1, Tabla 2, Tabla 3, Figura 2 y Tabla A4.
Los valores de la precipitación efectiva se observan en la Tabla 4. Esta información sirvió como datos de entrada para del Hidrograma Unitario Triangular de la SCS y el Hidrograma Unitario Sintético de Snyder, para estimar caudales máximos para diferentes tiempos de retorno.
Se utilizó la información de la Figura 3. Se utilizó las 8 funciones probabilísticas que ofrece el programa Hidroesta 2. Se estableció a la función probabilista Gama 3 parámetros, mediante la prueba de Smirnov- Kolmogorov. Esta función, estimó caudales máximos anuales para el río Jequetepeque para diferente tiempo de retorno, ver Tabla 5. Estos caudales máximos, serán objeto de comparación con los caudales máximos generados a partir de la información de data grillada espacial de lluvia llamada PISCO (Peruvian Interpolated data of SENAMHI's Climatological and Hydrological Observations).
Según Lauro et al. (2021) señala que, al contar con la información necesaria es posible generar caudales máximos para diferentes tiempos de retorno. Esto permitió estimar caudales máximos anuales partir del método del Hidrograma Triangular de la SCS, ver Tabla A3. Los componentes del mencionado método y sus respectivos valores se presentan en la Tabla A3.
La generación de caudales máximos para diferentes tiempos de retorno se estimó a partir del método HUS de Snyder, ver Tabla A4. Los componentes del mencionado modelo y sus respectivos valores se presentan en la Tabla A4 El valor del caudal pico total presentados en la Tabla A4, se multiplicó con la información de la Tabla 4. Esto permitió generar caudales máximos para diferente tiempo de retorno, ver Tabla A5.
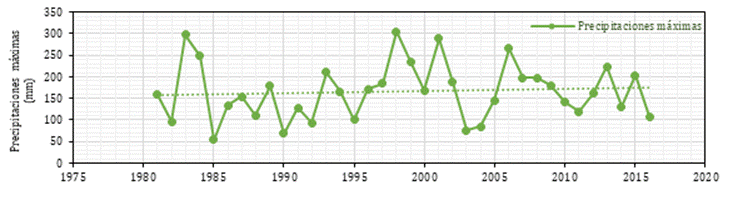
Figura 4. Precipitación máxima obtenida de la precipitación máxima mensual de data grillada 1981-2016.
Tabla 3
Precipitaciones máximas mensuales para diferentes tiempos de retorno
|
Distribución Probabilística |
Tiempos de retorno (años) |
|||||
|
5 |
50 |
100 |
200 |
500 |
1000 |
|
|
mm |
mm |
mm |
mm |
mm |
mm |
|
|
Gamma 3 parámetros |
219,08 |
314,13 |
337,51 |
359,48 |
386,78 |
406,14 |
|
Multiplicado por factor de corrección 1,13 |
||||||
|
Gamma 3 parámetros |
247,56 |
354,97 |
381,39 |
406,21 |
437,06 |
458,94 |
Tabla 4
Precipitación efectiva
|
Precipitación efectiva para el modelo HUT de la SCS |
||||||
|
Tiempos de retorno (TR) (años) |
||||||
|
|
5 |
50 |
100 |
200 |
500 |
1000 |
|
Pe (mm) |
109,34 |
179,23 |
196,82 |
213,45 |
234,22 |
249,02 |
|
Precipitación efectiva para el HUS de Snyder |
||||||
|
Tiempos de retorno (TR) (años) |
||||||
|
|
5 |
50 |
100 |
200 |
500 |
1000 |
|
Pe(mm) |
100,57 |
166,04 |
182,55 |
198,2 |
217,7 |
231,6 |
Tabla 5
Generación de caudales máximos para diferentes tiempos de retorno del río Jequetepeque
|
Distribución Probabilística |
Tiempos de retorno (años) |
|||||
|
5 |
50 |
100 |
200 |
500 |
1000 |
|
|
m3/s |
m3/s |
m3/s |
m3/s |
m3/s |
m3/s |
|
|
Gamma 3 parámetros |
153,97 |
236,57 |
256,52 |
275,15 |
298,19 |
314,46 |
La Tabla A5 muestra a caudales máximos gene-rados para diferente tiempo de retorno utilizando información de la Tabla A4, Tabla A3 y Tabla 4. Los datos de la Tabla A5, fueron comparados con la información de la Tabla 5.
Al realizar una comparación directa entre los caudales máximos anuales presentados en la Tabla 5 y Tabla A5, se evidenció una sobre estimación de caudales máximos anuales obtenidos con la data grillada espacial de lluvia de PISCO. Por tanto, para lograr un buen ajuste, entre los valores de los caudales máximos mencionados, se adecuó al Hidrograma Unitario Triangular de la SCS, es decir, la variable área de la cuenca fue afectado por un exponente igual a 0,483, cuyos resultados gene-rados se presentan en Tabla A6.
![]() (4)
(4)
Pe= Precipitación efectiva (mm), A=Área de la cuenca en estudios (km2), Tp=Tiempo pico (hora). Mediante un análisis visual, entre los resultados de la columna 3 y 4 de la Tabla A6, se evidenció una baja variabilidad. Para verificar esta variabilidad se usó el análisis estadístico a los resultados de la columna 3 y 4 de la Tabla A6, haciendo uso de indicadores estadísticos, tal como: las métricas presentadas en la columna 3 de la Tabla 6. Y las pruebas estadísticas, tales como: el coeficiente de determinación y Nash, presentados en la columna 1 de la misma tabla indicada. Se concluye que los resultados de la columna 3 y 4 de la Tabla A6, son próximos al valor ideal de cada estadístico de la columna 3 de la Tabla 6, es decir, presentan una baja variabilidad. De esta manera se establece que la Fórmula 4, genera caudales máximos anuales para diferentes tiempos de retorno para el río “Jequetepeque” de la cuenca alta.
La Tabla A2 muestra una baja variabilidad entre las precipitaciones mensuales observadas de la cuenca alta del Jequetepeque y la información de la data grillada del producto PISCO de Senamhi. Es decir, la Tabla A2 muestra que el indicador estadístico como el Coeficiente de Determinación (R2) comprende un rango entre 0,69 y 0,79. Según Roque Quiroz (2023) valores mayores a 0,61 indican buenos ajustes estadísticos. Por otro lado, Roque Quiroz (2023) también realizó una validación entre la precipitación observada de la cuenca de la Vertiente del Lago Titicaca (Lado peruano) con respecto a los datos del producto PISCO, mediante el indicador estadístico del Coeficiente de Determinación, se comprobó un buen ajuste con valores comprendidos entre 0,7 y 0,9. Carmona et al. (2021) demostró que entre las precipitaciones mensuales observadas de la cuenca del río Biabo y la data grillada del producto PISCO, presentan un Coeficiente de Determinación entre un rango de 0,60 y 0,90 y se comprobó un buen ajuste.
Por tanto, según la estadística presentada por las anteriores investigaciones y la estadística presen-tada en la Tabla A2, podemos indicar que la información de la data grillada del producto PISCO de Senamhi de la cuenca alta del Jequetepeque, puede ser utilizado para estudios hidrológicos, disponibilidad hídrica, análisis de eventos extremos, completación de datos faltantes y modelamiento hidrológico e hidráulico.
Al momento de utilizar la información del producto PISCO en los Hidrograma Unitario Triangular de la SCS y el Hidrograma Unitario sintético de Snyder, los resultados presentaron variabilidad con respecto al comportamiento real del caudal máximo anual en la estación hidrométrica Yonán del río Jequetepeque para diferentes tiempos de retorno, es decir, se evidenció una sobre estimación. Carmona et al. (2021) señala que es posible la aplicabilidad de la data grillada del producto PISCO y el uso del Hidrograma Unitario de Snyder para genera caudales máximos. Para Cunha et al. (2015) y Da Silveira (2016), los métodos estandarizados mencionados (hidrogra-mas unitarios), fueron elaborados para cuencas hidrográficas especificas (tamaño, relieve, uso y manejo del suelo). Estos métodos están basados en información fisiográfica, lluvia, número de curva y precipitación efectiva, y tienen una tendencia a sobreestimar caudales. Para generar caudales máximos anuales a partir del producto PISCO en la estación hidrométrica Yonán, se realizó una modificación a la variable área del Hidrograma Unitario Triangular de la SCS, es decir, se le agregó un exponente igual a 0,483. Esta modificación se realizó debido a la simplicidad de la expresión. Esta nueva expresión permitió obtener caudales máximos instaneos anuales para diferentes tiempos de retorno, que según la estadística presentada en la Tabla 6, los resultados son próximos a los caudales máximos observados del río Jequetepeque para diferentes tiempos de retorno. La investigación parte de la siguiente hipótesis: es posible estimar caudales máximos anuales para diferentes tiempos de retorno mediante el uso de hidrogramas unitarios en la cuenca alta del río Jequetepeque. Esta hipótesis se acepta ya que la información de la Tabla A6 fueron comparados mediante indicadores estadísticos de R2 y Nash (Tabla 6), y se demostró que están dentro de un rango aceptable de 0,98-0,99, evidenciando una baja variabilidad entre sus valores. Según Moncada & Willems (2020) y Krause et al. (2005) los indicadores estadísticos, son importantes para medir la eficiencia de un modelo.
Confiabilidad de los resultados mediante indicadores estadísticos
|
Indicador Estadístico (1) |
Valor (2) |
Rango (3) |
Valor ideal (4) |
|
R2 |
0,99 |
[0;1] |
1 |
|
NASH |
0,98 |
[-α;1] |
1 |
Se determinó el número de curva igual a 77,65 y el tiempo de concentración igual a 8,61 horas para la cuenca alta del Jequetepeque. La comparación de las precipitaciones máximas medios mensuales y las precipitaciones máximas medios mensuales del producto PISCO, presentaron una baja variabilidad según los indicadores estadísticos de R2 y Nash, lo cual permite utilizarlos en estudios hidrológicos. El producto PISCO aplicado al método del Hidrograma Unitario Triangular de la SCS y al Hidrograma Unitario Sintético de Snyder, generaron sobre estimación de caudales máximos. La data grillada del producto PISCO de Senamhi de la zona alta de la cuenca del Jequetepeque, son confiables para ser utilizado por el método del Hidrograma Unitario Triangular de la SCS, para generar caudales máximos anuales para diferente tiempo de retorno, pero con previa adecuación de la variable área (A) del mencionado método. Por la simplicidad de su expresión, se seleccionó al método del Hidrograma Unitario Triangular de la SCS señalado, para generar caudales máximos, al cual se le agregó un exponente en su estructura. Bajo esta modificación, el método seleccionado, generó caudales máximos anuales con baja variabilidad y un buen ajuste, con respecto a los caudales máximos anuales registrados por la estación hidrométrica Yonán ubicado en el río Jequetepeque.
Esta investigación demuestra que es posible adecuar al Método del Hidrograma Unitario Triangular de la SCS a las características de cada región del Perú. Asimismo, es posible utilizar el producto grillado PISCO de SENAMHI previa evaluación con información de estaciones terrestres. Para de esta manera estimar el caudal máximo de diseño hidráulico y estimación de evaluación de riesgo por inundación. Frente a la ausencia de estaciones de aforo en la costa, sierra y selva, es importante validar los datos grillados Pisco en zonas de carencia de equipamiento de aforo.
REFERENCIAS BIBLIOGRÁFICAS
Alejo, B. M., Tomas, K., Milagros, R. F., Inés, M. M., Alejandro, S. R., Guadalupe, R. R., Estefanía, G. V., Desiré, M. A., Alejo, B. M., Tomas, K., Milagros, R. F., Inés, M. M., Alejandro, S. R., Guadalupe, R. R., Estefanía, G. V., & Desiré, M. A. (2022). Regionalización de caudales máximos en subcuencas del arroyo Feliciano. Tecnología y Ciencia, 44, 1–25. https://doi.org/10.33414/RTYC.44.1-25.2022
Alvarez J, I., & Huamán J. F. (2024). Desempeño de métodos deterministas en la estimación del tiempo de concentración en la cuenca alta del Jequetepeque, Perú. Manglar, 21(4), 461-470. https://doi.org/10.57188/manglar.2024.050
Aybar Camacho, C., Lavado Casimiro, W., Huerta Julca, A., Fernández Palomino, C., Vega Jácome, F., Sabino Rojas, E., & Felipe Obando, O. G. (2017). Uso del producto Pisco de precipitación en estudios de investigaciones y sistemas operacionales de monitoreo del pronóstico hidrometeorológico. SENAMHI.
Ayuso, J. L., Peña, A., & Montesinos, M. P. (1994). Estimación del hidrograma unitario. Estudio comparativo de cuatro métodos lineales. Ingeniería Del Agua, 1(2). https://doi.org/10.4995/ia.1994.2635
Beven, K. J., & Hornberger, G. M. (1982). Assessing the effect of spatial pattern of precipitation in modeling stream flow hydrographS. JAWRA Journal of the American Water Resources Asociación, 18(5), 823–829. https://doi.org/10.1111/J.1752-1688.1982.TB00078.X
Boudrissa, N., Cheraitia, H., & Halimi, L. (2017). Modelling maximum daily yearly rainfall in northern Algeria using generalized extreme value distributions from 1936 to 2009. Meteorological Applications, 24(1), 114–119. https://doi.org/10.1002/MET.1610
Campos Aranda, D. F. (1998). Procesos del ciclo hidrológico. UASLP. San Luis Potosí, México, 20.
Castillo García, C. L., & Carvajal González, V. M. (2023). Modelación hidrológica de la cuenca urbana del río Bélico en la ciudad de Santa Clara, Cuba. Enfoque UTE, 14(2), 77-92. https://doi.org/10.29019/ENFOQUEUTE.888
Carmona Arteaga, A., Sarango Julca, D. D., & García Pérez, M. (2021). Generación de precipitaciones y caudales de máximas avenidas para las cuencas del río Biabo. Revista de Investigación de Física, 24(3). https://doi.org/10.15381/rif.v24i3.20920
Chen, L., Guo, S., Yan, B., Liu, P., & Fang, B. (2010). Un nuevo de inundación de diseño basado en la distribución conjunta bivariada de la magnitud de la inundación y de ocurrencia. Sciences Journal–Journal …, 55(8), 1264–1280. https://doi.org/10.1080/02626667.2010.520564
Chen, L., & Singh, V. P. (2017). Generalized beta distribution of the second kind for flood frequency analysis. Entropy, 19(6), 254. https://doi.org/10.3390/E19060254
Cunha, S., Silva, F., Mota, T., & Pinheiro, M. (2015). Avaliação da acurácia dos métodos do SCS para cálculo da precipitação efetiva e hidrogramas de cheia /Evaluation of the SCS method for effective rainfall and flood hydrograph estimation. Revista Brasileira de Recursos Hídricos, 20(4), 837–848. https://doi.org/10.21168/RBRH.V20N4.P837-848
Da Costa, F. F., da Paz, A. R., & Piccilli, D. G. A. (2019). Modified NRCS-CN-TUH methods for distributed rainfall-runoff modeling. RBRH, 24, e21. https://doi.org/10.1590/2318-0331.241920180104
Da Silveira, A. L. L. (2016). Fator de Pico para Hidrogramas Unitários Sintéticos Triangulares. RBRH, 21(1), 46–52. https://doi.org/10.21168/RBRH.V21N1.P46-52
Douka, M., Karacostas, T. S., Katragkou, E., & Anagnostolpoulou, C. (2017). Annual and seasonal extreme precipitation probability distributions at thessaloniki based upon hourly values. 521–527. https://doi.org/10.1007/978-3-319-35095-0_75
Espinales Cedeño, F. R., Alulema del Salto, R. A., Caicedo Toro, M. D., Espinales Cedeño, F. R., Alulema del Salto, R. A., & Caicedo Toro, M. D. (2021). Determinación del Número de Curva (CN) de la cuenca del Río Portoviejo. Dilemas Contemporáneos: Educación, Política y Valores, 8(SPE2). https://doi.org/10.46377/DILEMAS.V8I.2600
Espinosa-López, J. A., Ibáñez-Castillo, L. A., Arteaga-Ramírez, R., Galeana-Pizaña, J. M., Espinosa-López, J. A., Ibáñez-Castillo, L. A., Arteaga-Ramírez, R., & Galeana-Pizaña, J. M. (2024). Modelo hidrológico distribuido con imágenes GPM-IMERG en la cuenca del río Huaynamota, Nayarit, México. Tecnología y Ciencias Del Agua, 11(5), 344–383. https://doi.org/10.24850/J-TYCA-2020-05-09
Guo, S., Chen, L., Singh, V. P., Asce, S. M., Asce, F., Shenglian, G., Hao, Z., & Li, T. (2012). Análisis de riesgo de coincidencia de inundaciones utilizando funciones de cópula multivariadas. Journal of Hydrologic, 17(6), 742–755. https://doi.org/10.1061/(ASCE)HE.1943-5584.0000504
Krause, P., Boyle, D. P., & Bäse, F. (2005). Comparison of different efficiency criteria for hydrological model assessment. Advances in Geosciences, 5, 89–97. https://doi.org/10.5194/ADGEO-5-89-2005
Lauro, C., Vich, A., Moreiras, S. M., Bastidas, L., Otta, S., & Vaccarino, E. (2021). Regionalización del caudal máximo anual en cuencas del sistema hidrográfico del río Colorado, Argentina. Cuadernos de Investigación Geográfica, 47(2). https://doi.org/10.18172/cig.4465
Méndez, W., Córdova, J., & Bravo de Guenni, L. (2015). Modelos predictivos de caudales máximos instantáneos para cuencas de drenaje de ambientes montañosos, sustentados en parámetros morfométricos. Revista Técnica de La Facultad de Ingeniería Universidad Del Zulia, 38(3), 229–238.
Młyński, D., Wałȩga, A., Petroselli, A., Tauro, F., & Cebulska, M. (2019). Estimating maximum daily precipitation in the upper vistula basin, Poland. Atmosphere, 10(2), 43. https://doi.org/10.3390/ATMOS10020043
Moncada, W., & Willems, B. (2020). Tendencia anual del caudal de salida, en referencia al caudal ecológico en la microcuenca apacheta / Ayacucho / Perú, del 2000 al 2018. Ecología Aplicada, 19(2), 93. https://doi.org/10.21704/REA.V19I2.1560
Pedroso, A., & Mannich, M. (2021). The uncertainties of synthetic unit hydrographs applied for basins with different runoff generation processes. RBRH, 26, e38. https://doi.org/10.1590/2318-0331.262120210093
Portuguez, M., & Verano, C. (2016). Generación de mapa de número de curva con sistema de información geográfica. Apuntes de Ciencia & Sociedad, 6(1). https://doi.org/10.18259/acs.2016029
Rivasplata Flores, L. F. (2019). Generación de escorrentía superficial a partir de información climática en la cuenca de la quebrada Huertas - Chilete, Cajamarca. Tesis profesional. Universidad Nacional de Cajamarca.
Roque Quiroz, R. A., & Roque Quiroz, R. A. (2023). Validación de la data de precipitación (1981-2016) del producto PISCO v2.1: Estación meteorológica, elevación, estacionalidad del año y región climática en la cuenca Tumbes, Perú. Manglar, 20(1), 41–50. https://doi.org/10.57188/MANGLAR.2023.005
Shao, Q., Wong, H., Xia, J., & Ip, W.-C. (2004). para extremos utilizando Burr XII extendido de tres parámetros con aplicación al de de crecidas/Modèles d’extrêmes utilisant le système Burr XII... Revista de Ciencias Hidrológicas, 49(4). https://doi.org/10.1623/hysj.49.4.685.54425
Skidelsky, D., Villaverde, A. G., Mastaglia, M. I., Ramirez, R., Sato, R., Gimenez, V., & Margasin, A. (2023). Regionalización de caudales máximos mediante técnicas estadísticas multivariadas en cuencas de la provincia de Entre Ríos. Revista de Geología Aplicada a La Ingeniería y al Ambiente, 50, e002. https://doi.org/10.59069/24225703E002
Sousa Rocha, J., Duarte Souza Carneiro, B. L., Costa Malveira, V. T., & Lima Neto, I. E. (2021). Modelo de regionalização de hidrogramas unitários para bacias hidrográficas do Ceará. Revista DAE, 69(233), 86–104. https://doi.org/10.36659/DAE.2021.079
Ticse De la Torre, J., & Moya Álvarez, A. S. (2019). Dinámica de lluvias extremas en el centro y norte del Perú, vertiente del Pacífico para febrero y marzo de 2017. Repositorio Institucional - IGP, 6(9).
Tye, M. R., & Cooley, D. (2015). A spatial model to examine rainfall extremes in Colorado’s Front Range. Journal of Hydrology, 530, 15–23. https://doi.org/10.1016/J.JHYDROL.2015.09.023
Upegui, J. J. V., & Gutiérrez, A. B. (2011). Estimación del tiempo de concentración y tiempo de rezago en la cuenca experimental urbana de la quebrada san Luis, manizales. DYNA (Colombia), 78(165).
Vélez, J. J., Botero, B. A., Parra, J. C., Aristizabal, V. M., & Marulanda, A. (2012). Diseño hidráulico e hidrológico de obras de ingeniería para proyectos viales. https://repositorio.unal.edu.co/handle/unal/82744
Videla Valdebenito, M. P. (2023). Diseño hidrológico de las defensas fluviales del río Camiña en un contexto de cambio climático: Camiña, Chile. https://doi.org/10.58011/KZ24-GD61
Villazón Gómez, J. A., Noris, P., Martín Gutiérrez, G., Villazón Gómez, J. A., Noris Noris, P., & Martín Gutiérrez, G. (2021). Determinación de la precipitación efectiva en áreas agropecuarias de la provincia de Holguín. Idesia (Arica), 39(2), 85–90. https://doi.org/10.4067/S0718-34292021000200085
Wałȩga, A. (2016). The importance of calibration parameters on the accuracy of the floods description in the Snyder’s model. Journal of Water and Land Development, 28(1), 19–25. https://doi.org/10.1515/JWLD-2016-0002
ANEXOS
Tabla A1
Tiempo de concentración mediante modelos determinísticos para la cuenca alta del Jequetepeque (Alvarez & Huamán, 2024)
|
Métodos |
|
Tiempo de concentración (Tc) (h) |
|
Kirpich-Tennessee (1940) |
|
7,82 |
|
Johnstone and Cross (1949) |
|
10,23 |
|
Giandotti (1934) |
|
10,88 |
|
Ven te Chow (1962) |
|
8,44 |
|
Cuerpo de ingenieros USA (1954) |
|
11,39 |
|
California (1955) |
|
7,84 |
|
Valencia y Zuluaga |
|
7,39 |
|
Rziha (1876) |
|
9,44 |
|
Yoon & Park (2002) |
|
6,87 |
|
Jung (2005) |
|
8,24 |
|
Kim (2015) |
|
6,16 |
|
Promedio |
|
8,61 |
Tabla A2
Variabilidad entre las precipitaciones máximas mensuales de estaciones meteorológicas terrestres y la data grillada espacial
|
Estación |
R2 |
msnm |
Condición |
|
Contumazá |
(R2=0,73) |
2440 |
Baja variabilidad |
|
Chilete |
(R2=0,69) |
805 |
Baja variabilidad |
|
Monte Grande |
(R2=0,74) |
431 |
Baja variabilidad |
|
Asunción |
(R2=0,74) |
2160 |
Baja variabilidad |
|
Cospán |
(R2=0,68) |
2300 |
Baja variabilidad |
|
San Juan |
(R2=0,79) |
2185 |
Baja variabilidad |
|
Llagaden |
(R2=0,37) |
2150 |
Alta variabilidad |
|
San Pablo |
(R2=0,79) |
2190 |
Baja variabilidad |
Tabla A3
Valores y componentes usados en el método HUT de la SCS
|
Descripción |
Unidad |
Expresión |
Componentes |
Valores |
|
Duración de lluvia efectiva |
hora |
|
Tc: Tiempo de concentración (hora) |
5,86 |
|
Tiempo de rezago |
hora |
|
Tc: Tiempo de concentración (hora) |
5,17 |
|
Tiempo pico |
hora |
|
de: Duración de lluvia efectiva (hora) |
8,10 |
|
Lamina de lluvia neta |
mm |
|
TR: Tiempo de rezago: |
174,08 |
|
Caudal máximo |
m3/s |
|
de: Duración de lluvia efectiva |
En función del área y precipitación efectiva |
Tabla A4
Valores y componentes usados en el método HUS de Snyder
|
Descripción |
Unidad |
Expresión |
Componentes |
Valores |
|
Tiempo de rezago |
hora |
|
Lc: Longitud del cauce principal (pies); S: factor de retención (pulgadas); Sc=pendiente de la cuenca (porcentaje) |
25,61 |
|
Duración de lluvia |
hora |
|
TR=Tiempo de rezago (horas) |
4,66 |
|
Tiempo pico |
hora |
|
Tc=Tiempo de concentración (horas); TR=Tiempo de rezago (horas) |
29,92 |
|
Tiempo base en días |
días |
|
TR=Tiempo de rezago (horas) |
6,20 |
|
Duración de la precipitación efectiva del hidrograma |
hora |
|
Tc=Tiempo de concentración (horas) |
1,15 |
|
Caudal pico por unidad de área |
(ft3/ (s.mi2.in)) |
|
TR=Tiempo de rezago (horas); T: Duración de la precipitación efectiva del hidrograma (hora); mi=milla, Ts=Duración de lluvia; Cp= Factor de pendiente del terreno de la cuenca (0,5-0,8). |
16,82 |
|
Caudal pico total |
m3/(s.mm) |
|
A=Área de cuenca (mi2) up=Caudal pico por unidad de área |
23,85 |
Tabla A5
Caudal máximo instantáneo
|
Caudal máximo instantáneo obtenido por el Hidrograma Unitario Triangular de la SCS |
|||||||
|
TR |
Años |
5 |
50 |
100 |
200 |
500 |
1000 |
|
Pe |
(mm) |
109,34 |
179,23 |
196,82 |
213,45 |
234,22 |
249,02 |
|
Caudal Pico |
m3/s |
9249,94 |
15163,31 |
16651,62 |
18058,00 |
19815,40 |
21067,19 |
|
Caudal máximo instantáneo obtenido por el Hidrograma Sintético de Snyder |
|||||||
|
TR |
Años |
5 |
50 |
100 |
200 |
500 |
1000 |
|
Pe |
mm |
100,57 |
166,04 |
182,55 |
198,2 |
217,7 |
231,6 |
|
Caudal Pico |
m3/s |
2398 |
3960 |
4354 |
4726 |
5192 |
5523 |
Tabla A6
Caudal máximo generado por Hidrograma Unitario Triangular de la SCS modificado
|
Tiempo de retorno (1) |
Precipitación efectiva (2) mm |
Caudal máximo observado (3) m3/s |
Caudal máximo (fórmula 4) (4) m3/s |
|
5 |
109,34 |
153,97 |
140,43 |
|
50 |
179,23 |
236,57 |
230,19 |
|
100 |
196,82 |
256,52 |
252,78 |
|
200 |
213,45 |
275,15 |
274,13 |
|
500 |
234,22 |
298,19 |
300,81 |
|
1000 |
249,02 |
314,46 |
319,82 |