 |
INTRODUCCIÓN
Uso del producto global (GCN250) para la identificación del Número de Curva (CN) en la cuenca alta del Jequetepeque, Perú
Use of the global product (GCN250) for the identification of the Curve Number (CN) in the upper Jequetepeque watershed, Peru
Jairo Isaí Alvarez Villanueva1; José Francisco Huamán Vidaurre1
* Autor corresponsal: jialvarezv@unc.edu.pe (J. I. Alvarez Villanueva).
ORCID de los autores
J. I. Alvarez Villanueva: https://orcid.org/0000-0001-8777-3943
J. F. Huamán Vidaurre: https://orcid.org/0000-0002-4896-0479
RESUMEN
El objetivo de la investigación fue usar el producto global (GCN250) para identificar el Número de Curva en la cuenca alta del Jequetepeque, Perú. La investigación identificó el Número de Curva, a partir de información del producto Número de Curva (NC) a escala global denominados GCN250, y apoyado del Sistema de Información Geográfica (SIG) Qgis 3.42.0. EL producto global permitió identificar tres condiciones en la cuenca en estudio, estos son: seca, promedio y húmedo. Estas condiciones representadas en mapas permiten visualizar la distribución especial del número de curva aún no validados y demuestran la temporalidad del NC. Se obtuvo valores promedios del NC para cuenca alta del Jequetepeque bajo las siguientes condiciones: condición seca ARC I es de 56, 96, para la condición promedio ARC II es de 74,5 y para la condición humedad ARC III es de 86,53. Además, se identificó el NDVI para la zona de producción de sedimentos para la cuenca en estudio igual a -0,3 a 0,2. Asimismo, se determinó el NC para la mencionada zona para las diferentes condiciones ARC I es de 58 a 60, para la condición promedio ARC II es de 76 a 77 y para la condición humedad ARC III es de 89. La información de GCN250 permite validar y refinar los valores de NC a través de datos hidrológicos mas específicos de la zona.
Palabras clave: Numero de curva; producto global GCN250; cuenca alta del Jequetepeque.
ABSTRACT
The objective of the research was to use the global product (GCN250) to identify the Curve Number in the upper Jequetepeque basin, Peru. The research identified the Curve Number based on information from the global Curve Number (CN) product called GCN250, supported by the Geographic Information System (GIS) Qgis 3.42.0. The global product made it possible to identify three conditions in the basin under study: dry, average, and wet. These conditions, represented on maps, allow the special distribution of the curve number to be visualized, even though it has not yet been validated, and demonstrate the temporality of the CN. Average CN values were obtained for the upper Jequetepeque basin under the following conditions: dry condition ARC I is 56.96, for the average condition ARC II is 74.5, and for the wet condition ARC III is 86.53. In addition, the NDVI for the sediment production area for the basin under study was identified as -0.3 to 0.2. Likewise, the CN for the mentioned area was determined for the different conditions: ARC I is 58 to 60, for the average condition ARC II is 76 to 77, and for the humidity condition ARC III is 89. GCN250 information allows the CN values to be validated and refined using more specific hydrological data for the area.
Key words: Curve number; global product GCN250; upper Jequetepeque basin.
Recibido: 26-06-2025.
Aceptado: 08-09-2025.
El método del Número de Curva o conocido como Curva Número fue desarrollado por el Servicio de Conservación de Suelos de los Estados Unidos en 1954, es ahora conocido como el Servicio de Conservación de Recursos Naturales (NRCS), por sus siglas en inglés) (Sobral et al., 2025). EL número de curva es un índice adimensional, utilizado para identificar el potencial hídrico de un área, debido a los eventos de lluvia (Alivio et al., 2024). La variación del NC esta influenciado por los diferentes eventos de tormentas relacionados con la cantidad de lluvia, intensidad y duración (Pérez-Corredor et al., 2024). Número de Curva del Servicio de Conservación de Recursos Naturales (NRCS-CN) es conocida por su simplicidad y por estimar la escorrentía a partir de eventos de lluvia en cuencas hidrográficas calibradas y no calibradas (Mishra et al., 2018). El Número de Curva es un método propuesto por el Servicio de Conservación de Suelos (SCS-CN) (Zhang et al., 2018). Es un método empírico muy utilizado para estimar caudales en cuencas no aforadas (Assaye et al., 2021). El modelo de lluvia – escorrentía Número de Curva (CN), fue desarrollado por el Departamento de Agricultura de los Estados Unidos (USDA) y el Servicio de Conservación de Suelos (SCS) en el año de 1954, y (Lee et al., 2023). El método de NC, es el método más utilizado. Fue desarrollado tomando como base a las máximas lluvias y escorrentías de 200 cuencas hidrográficas de 23 estados de los EE. UU. El modelo fue desarrollado para implementar actividades en proyectos de: control, protección, prevención de inundaciones y manejo y conservación de cuencas hidrográficas (Sobral et al., 2025).Este método permite calcular la cantidad de escorrentía de una tormenta (Serie de capacitación en hidrología para ingeniería del NEDC, [SCHI-NEDC]1997). El método de número de curva (NC) permite realizar el modelamiento hidrológico para estimar la escorrentía (Jaafar et al., 2019). Es un método utilizado para determinar la cantidad de lluvia efectiva generada por una tormenta en una zona específica de estudio (Espinales Cedeño et al., 2021). Es un parámetro hidrológico que indica la capacidad de infiltración de un terreno de una unidad hidrográfica o de generar escorrentía superficial directa en suelos no congelados (Pacheco Moya et al., 2018). El número de curva (NC) es el método más usado para estimar escorrentía superficial, su estimación se puede realizar mediante el uso del sistema de información geográfica (García-Guerrero et al., 2021). El producto GCN250 ofrece valores de NC en cuadrículas, el cual utiliza la cobertura terrestre (Alivio et al., 2024). La geología es significativo para realizar el análisis hidrológico. Los cambios en la cobertura del suelo influyen en el cálculo del valor del número de curva (NC) del Servicio de Conservación de Suelos (SCS) (Theochari & Baltas, 2024).
La selección de los valores del NC, aún está en debate para las cuencas hidrográficas de todo el mundo, específicamente en cuencas hidrográficas con pendiente pronunciada con entornos ambientales diversos (Ajmal et al., 2020). El uso del sistema de información geográfica (SIG) para la estimación del número de curva permite utilizar diversa información dentro de una misma área de estudio. El SIG, permite presentar el valor del número de curva (NC), a través de planos a escala regional (Ferrer et al., 1995). Los factores que influyen en la determinación del parámetro hidrológico de numero de curva, son: el uso de suelo / cobertura de suelo, el grupo hidrológico del suelo, las condiciones de humedad, las condiciones hidrológicas de la zona y las prácticas de cultivo del área de estudio, siendo los dos primeros los más importantes (Ferrer-Juliá, 2002). El NC se estima considerando los siguientes dos factores: grupo hidrológico de suelo de la zona, el uso y cobertura del suelo. Asimismo, se hace un estudio de las condiciones hidrológicas la zona de estudio y contenido de humedad (Hong & Adler, 2008) (Ekwule & Agunwamba, 2024). Existen grupos hidrológicos denominados en grupos A,B,C y D, estos grupos están ordenados de mayor a menor capacidad de infiltración. Por otro lado, los valores de CN, presentados en las tablas generadas por el método SCS, corresponden a las condiciones CN (I) seca, CN (II) (media) y CN (III) (húmeda). Lo mencionado anteriormente, describen cuando húmedo estaba el suelo antes de una tormenta, los cual está relacionado a cuanta lluvia puede convertirse en escorrentía (García-Guerrero et al., 2021).
Evaluar la infiltración es importante para lograr estimar la escorrentía superficial, siendo el método del número de curva (NC) el modelo más usado (García-Guerrero et al., 2021) El número de curva está en función de la permeabilidad (capacidad de infiltración del suelo) el uso (cobertura del suelo) y otras condiciones generadoras de escorrentía en una unidad hidrográfica. El NC cuantifica la escorrentía directa conociendo la altura de la lámina de lluvia acumulada. El número de curva es adimensional y valor está en el rango de 0 a100. Los valores de NC, que se presentan en tablas están en función de los tipos de suelo y cobertura terrestre (Hawkins et al., 2019). El número de curva permite cuantificar la escorrentía directa en áreas de cuencas, y permite mejorar la modelación hidrológica (Alivio et al., 2024). El NC representa el potencial de una cuenca para generar escorrentía superficial. Un valor de NC alto, indica mayor probabilidad de escorrentía, el cual está asociado a una superficie impermeable o suelos precariamente drenados. Un valor de NC bajo, indica mayor infiltración y menor escorrentía. Esta característica ultima, es observada en áreas forestales o agrícolas, óptimamente drenadas (Ekwule & Agunwamba, 2024). Las inundaciones son desastres naturales causados por exceso de lluvia no absorbido por el suelo, generando grandes masas de agua que terminan en desbordamientos e inundaciones. Por tanto, es importante entender la relación entre lluvia y escorrentía, con la finalidad de tener una mejor predicción de la escorrentía (Lee et al., 2023) Los cambios de uso de suelo, es decir, de la agricultura a una superficie impermeable, genera que aumente los niveles de la escorrentía (Zhang et al., 2018)- Estudios han demostrado que existen diferencias entre los valores del NC tabulados y los observados en las cuencas hidrográficas (Hawkins et al., 2014).Respecto a los valores altos del NC, estos están regidos por la variación espacial de la pendiente, la precipitación y la presencia de limo del suelo. Por otro lado, valores de NC más bajos están influenciados por las tierras forestadas relacionados a regiones de suelos arenosos con índice de aridez (Brandão et al., 2025). El NC tiene un desempeño bajo, irregular e inconsistente en cuencas forestadas y en cuencas con lluvias frecuentes de bajo volumen y baja intensidad. Asimismo, el investigador señala que el NC tiene problemas con los valores tabulados del NC para cuencas con áreas de gran cubierta vegetal y zonas forestales húmedas. Para los contextos indicados, el modelo de NC no es aplicable para estimar escorrentía (Tedela et al., 2011). El NC es más complejo cuando se presenta entornos naturales difíciles, tales como, las cuencas de cobertura vegetal densa. Po tanto, bajo estas condiciones es necesario realizar ajustes para cada región con entornos complejos (Lian et al., 2020). No hay un acuerdo en que señale que las cuencas hidrográficas con mayor pendiente deberían tener mayores valores de NC (Huang et al., 2006). Los valores de NC de tablas de manual son más efectivos en cuencas agrícolas de secano, menos eficientes en cuencas semiáridas y menos exitosos en cuencas forestadas (Kowalik & Walega, 2015). El número de curva (NC) es un parámetro que permite ser usado en el diseño hidrológico para cuantificar cambios en la escorrentía (Pérez-Corredor et al., 2024). Los aumentos de volumen de escorrentía son generados por la disminución de infiltración, una menor profundidad de almacenamiento de agua y encharcamiento por saturación del suelo y por elevadas velocidades de flujo superficial (Deshmukh et al., 2013). El modelo NC se utiliza para predecir la escorrentía de cuencas hidrográficas no aforadas. El uso de valores tabulados del NC para generar escorrentía presentó incertidumbres en 10 cuencas hidrográfica con características hidrográficas montañosas y boscosas en el este de los Estados Unidos (Tedela et al., 2011). Debido a la disponibilidad de información de la cobertura terrestre, se desarrolló el número de curva global de resolución espacial aproximada de 250 m (GCN250), el cual es un producto de datos que permite realizar evaluaciones temporales a escala global (todo el planeta), regional (comprende un continente o un país) y de cuencas hidrográficas, útil para realizar: diseño hidrológico, mapeo de riesgo por inundación, gestión hídrica en cuenca hidrográficas en otras. La distribución global del número de curva abarca cuenca del Amazonas, Misisipi, Mekong, Nilo y Tigris -Éufrates (Jaafar et al., 2019). El uso del producto global (GCN250) permite dar mayor precisión a los modelos hidrológicos para la gestión de aguas pluviales (Alivio et al., 2024). El propósito de la investigación es identificar el número de curva NC para la cuenta alta del Jequetepeque. Para esto se utilizó el sistema de información geográfica.
METODOLOGÍA
Área de estudio
El área de estudio (Figura 1) tiene un área de 3304,96 km2. Un perímetro de 379,56 km. La máxima elevación es 4229 msnm y la mínima elevación es 445 msnm. La elevación media es de 2587 msnm. Asimismo, el área mencionada se ubica en la cuenca alta del río Jequetepeque. La mencionada área es la principal zona de aporte hídrica para el embalse “Gallito Ciego”. La mencionada área se delimitó con el programa SIG libre Qgis 3.42.0 y con la ayuda de un complemento denominado ArcGeek Calculator. El siguiente enlace, permite descargar versiones de Qgis: https://download.qgis.org/downloads/.
Imágenes satelitales
Para la delimitación de cuenca, se usó imágenes del satélite ALOS. Este satélite, es operado por la Agencia Japonesa de Exploración Aeroespacial (JAXA), cuenta con un sensor llamado PALSAR, que permite obtener imágenes de la superficie terrestre. Las imágenes, tienen una buena resolución espacial de 12,5 metros, lo que resulta útil para diversos estudios hidrológicos. Las imágenes ALOS PALSAR, se descargan del siguiente enlace: https://search.asf.alaska.edu/#/. Para poder visualizar el mapa global de cobertura terrestre con una resolución de 10 m, basado en datos de los satélites Sentinel-1 y Sentinel-2. El enlace al visualizador de ESA WorldCover 2020, es:
https://viewer.esa-worldcover.org/worldcover/. Los mapas de cobertura de suelo y vegetal se obtuvieron de https://www.geogpsperu.com/ cuya fuente es el Ministerio del Ambiente (MINAM).
Los mapas utilizados en este trabajo se obtuvieron a partir de imágenes del satélite ALOS, que fue lanzado en enero de 2006. Este satélite, operado por la Agencia Japonesa de Exploración.
Datos globales de número de curva GCN250
Según Jaafar et al., (2019) los datos de número de curva global denominados como GCN250 tienen una resolución espacial aproximada de 250 m. Esta información necesito de datos globales de cobertura terrestre (300m) y suelo de (250m). Estas imágenes utilizan el sistema de coordenadas geográficas datum del Sistema Geodésico Mundial 1984 (WGS84). Los datos globales de número de curva están en formato Geotiff, ver enlace: https://doi.org/10.6084/m9.figshare.7756202
En base a la propuesta de Jaafar et al. (2019), es decir, en base a la información global del producto GCN250 se generó mapas de número de curva para la cuenca alta del Jequetepeque.
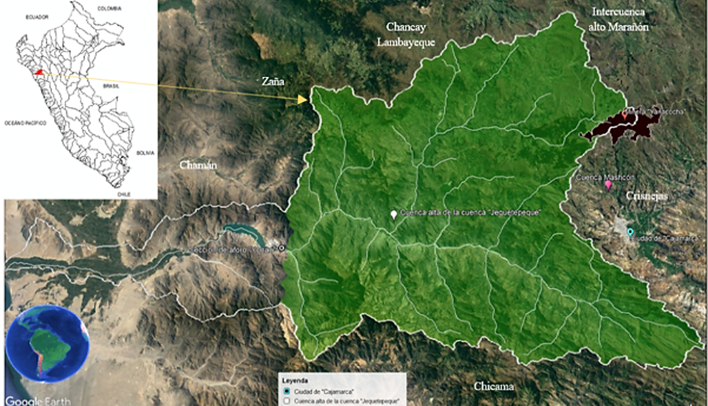
Figura 1. Cuenca alta del Jequetepeque. Fuente: (Alvarez Villanueva et al., 2024).
Jaafar et al. (2019) lograron un mapa con una alta resolución, debido al uso de la siguiente información: producto de precipitación en cuadrícula del Sistema Global de Asimilación de Datos Terrestres (GLDAS) https://disc.gsfc.nasa.gov/datasets/GLDAS_NOAH025_3H_2.1/summary, datos de cobertura terrestre global de la Agencia Espacial Europea (ESA), conocido como ESA CCI-LC. Estos tienen una resolución espacial de 300 metros y fue ajustado a 250 metros de resolución para el modelo global. Asimismo, utilizó el conjunto de datos de HYSOGs250m, esta información brindó una clasificación global de suelos en cuatro grupos hidrológicos (A, B, C y D), los cuales están relacionados a su capacidad de infiltración y textura. La mencionada información presenta una resolución espacial de aproximadamente 250. Podemos señalar que para la generación del producto GCN250, se utilizó las tablas de referencia de número de curva del USDA (método USDA).
Mapa de número de curva mediante el método USDA (SCS)
Se utilizó la metodología USDA, mediante la intercepción espacial de mapas de uso de suelo y su porcentaje de grupo hidrológico del suelo, y con mapas de cobertura vegetal. Para poder crear mapa de número de curva con el método indicado, se utilizaron mapas de usos de suelo (relacionado al tipo de aprovechamiento actual del suelo o su potencial en superficie y tipos de suelo (relacio-nado a su composición pedológico y su litología).
Número de curva mediante el producto GCN250 para la cuenca alta del Jequetepeque
Para la generación de mapas de Número de curva se utilizó la herramienta SIG Qgis 3.42.0 y los tres escenarios propuestos por Jaafar et al. (2019), tres mapas a escala mundial del producto números de curva global (GCN250), estos son: (a) Condiciones de escorrentía antecedentes secas (ARCI), (b) promedio (ARCII) y (c) húmedas (ARCIII).
Delimitada la cuenca alta del Jequetepeque se determinó el Número de Curva (NC) (Figura 2). De la Figura 2, el valor promedio del NC es 77,65. Si bien estos mapas presentan una buena resolución espacial, la extensión de la cobertura espacial es muy generalizadas y no reflejan la heterogeneidad del Número de Curva. La poca heterogeneidad, resulta adecuado para estudios preliminares a escala regional.
El mapa de NC presentado en la Figura 2, presenta una limitación en la categorización de los valores de numero de curva, ya que no cuenta con una actualización temporal y una validación de campo, causando errores en su interpretación. Esto puede limitar la precisión de los modelos hidrológicos detallados. Según Jaafar et al. (2019), el producto GCN250, presenta una resolución de 250 m incorpora el método estandarizado USDA, cobertura terrestre y grupo hidrológico de suelos para asignación del NC. Asimismo, integra datos globales de uso de suelo y grupos hidrológicos de suelo, lo que permite una estimación de valores más amplios para ser usados en análisis hidrológico. Pacheco Moya et al. (2018) señala que realizar este cálculo de manera manual, con lleva a utilizar una gran cantidad de información espacialmente distribuida, por lo cual se recurre al uso del SIG.
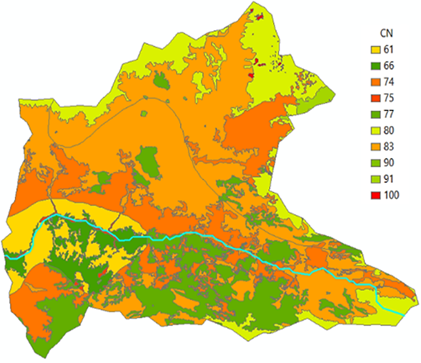
Figura 2. Mapa de distribución de valores de NC, en base al método USDA y SIG.
Para tener una mejor visualización de la distribución del número de curva, se modificó la categoría al rango de valores de la Figura 3. Esto se realizó con la finalidad de tener una mejor visibilidad de los valores de número de curva, los valores mencionados presentan un valor mínimo de 36 y valor máximo de 81 para un escenario seco. Es importante señalar que el tamaño de la celda X, Y es de 0,002083333 grados. Como el mapa global del NC propuesto por Jaafar et al. (2019) presenta una resolución aproximada de 250 m, entonces, la Figura 3 presentará la misma resolución aproxi-mada. La estadística de los valores de Número de curva para condición seca de la Figura 2, son 12 valores de NC dentro de la zona de estudio, el mínimo valor es 36 y el máximo valores es de 81. El promedio es de 56,96. La desviación estándar es de 12,364. A diferencia de la Figura 2, donde no se especifica la condición del escenario, Jaafar et al. (2019) propone 3 condiciones de diferencias espaciales significativas y escenarios temporal, entre ellos la condición seca, NC (I). Según los autores el NC global para la condición seca ARC I es de 62, este valor se aproxima al identificado para la cuenca alta del Jequetepeque para la indicada condición. Además, el número de curva identificado para la zona de producción de sedimentos para la condición seca ARC I, le corresponden valores de 76 a 77.
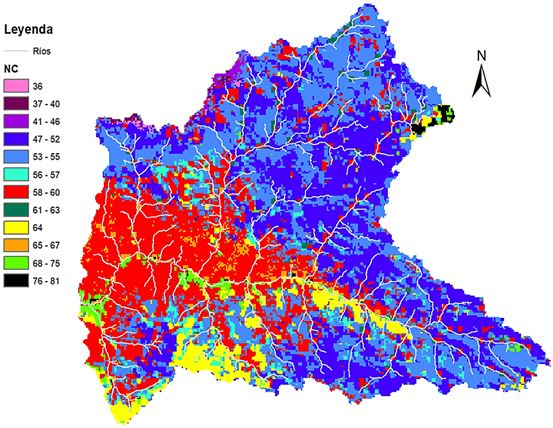
Figura 3. Distribución de valores de NC para condiciones de escorrentía antecedentes secas (ARC I).
La Figura 4 representa una zona de mayor producción de sedimentos, que afecta al embalse Gallito Ciego, parte baja de la cuenca. Esta zona presenta un NDVI de -0,3 a 0,2. Mejia et al. (2021), señalan que valores dentro de este rango corresponde a zonas sin vegetación, agua o sombras. La estadística de los valores de Número de curva para condición promedio de la Figura 5, son 12 valores de NC dentro de la zona de estudio, el mínimo valor es 56 y el máximo valores es de 92. El promedio es de 74,5. La desviación estándar es de 9,84. El análisis estadístico indica una dispersión moderada alrededor del promedio del valor de NC=74,5. Es decir, una capacidad moderada en la capacidad de escorrentía superficial dentro de la cuenca.
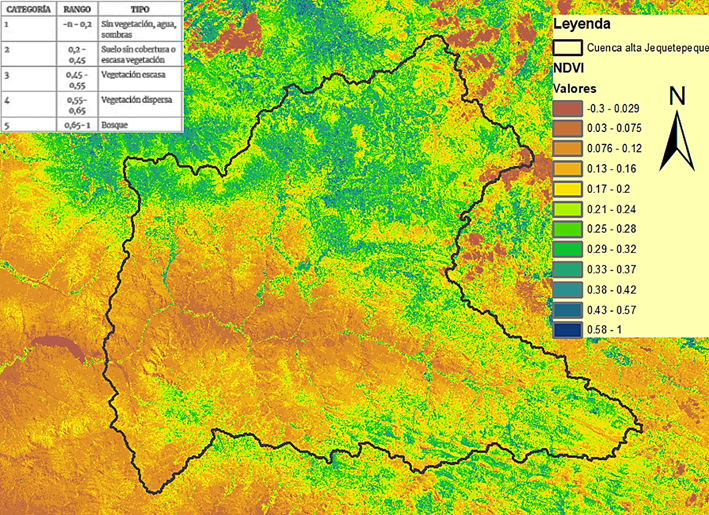
Figura 4. Mapa de distribución de valores de NDVI.
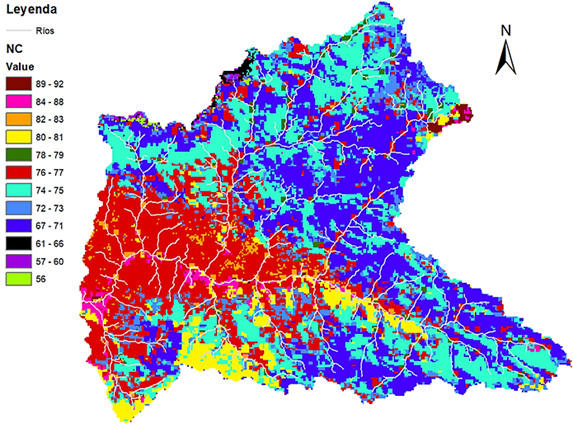
Figura 5. Distribución de valores de NC para condiciones de escorrentía antecedentes promedio (ARCII).
Asimismo, la dispersión de valores refleja la heterogeneidad espacial en el uso de suelo que afectan directamente a la infiltración y al comportamiento hidrológico. Esta variabilidad sugiere que, aunque la mayoría de los datos se concentran cerca del promedio, existe una heterogeneidad significativa en la distribución de los valores de NC, reflejando diferencias espaciales o temporales. Por tanto, al utilizar estos datos para modelación hidrológica, análisis ambiental o toma de decisiones, es fundamental considerar esta dispersión para evitar generalizaciones excesivas y asegurar que las conclusiones sean precisas y representativas con respecto a la diversidad real dentro de la cuenca estudiada García-Guerrero et al. (2021) señalan que la mayor variación del Número de Curva se da por la asignación de valores en el grupo hidrológico. Además, Jaafar et al. (2019) recomiendan complementar información detallada local in situ, para mejorar la precisión del valor del NC y tener mayor precisión de la escorrentía y la gestión de recursos hídricos. A diferencia de la Figura 1, donde no se especifica la condición del escenario, Jaafar et al. (2019) proponen 3 condiciones de diferencias espaciales y escenarios temporales, entre ellos el escenario promedio, NC (II).
Jaafar et al. (2019) determinaron que en el mundo predomina un potencia de escorrentía de medio alto, con NC comprendidos entre 75 y 85. Además indican que el valor de NC global para la condición humedad ARCII es de 78. Hope& Schulze (1982) indica que los valores del NC obtenidos de las tablas generadas por el método del SCS corresponden a condiciones medias, CN(II). Según Diaz Carvajal & Mercado Fernández (2017) señalan que valores altos de NC, indican condiciones que favorecen a la formación de escorrentía superficial por encima de la infiltración. Y que una escorrentía sin ningún control conduce a la degradación del suelo y el agua, propiciando la desertificación.
La estadística de los valores de Número de curva para condición húmeda de la Figura 6, son 12 valores de NC dentro de la zona de estudio, el mínimo valor es 75 y el máximo valores es de 97. El promedio es de 86,53. La desviación estándar es de 6,28, el cual es relativamente baja en comparación con las dos desviaciones estándar estimadas. Este valor indica que los datos están concentrados alrededor de la media, es decir, no hay una variabilidad en la información del NC. A diferencia de la Figura 1, donde no se especifica la condición del escenario, Jaafar et al. (2019) propone 3 condiciones de diferencias espaciales y escenarios temporal, entre ellos una condición seca, NC (I) con un valor de 62, la condición promedio NC (II) con un valor de 78 y la condición húmeda NC (III) cuyo valor es de 90. Teniendo en cuenta los datos de Jaafar et al. (2019), el NC global para la cuenca alta del Jequetepeque corresponde a una condición de escenario húmedo NC (III).
Para Jaafar et al. (2019) los datos presentados en el producto GCN250 no están validados para determi-nadas zonas del mundo, y que solamente es una aproximación de los valores de NC. También señala que antes de elegir los productos GCN250 (ARCI, ARCII y ARCIII), debemos tener conocimientos de sobre el uso de suelo de la unidad hidrográfica, intensidad de precipitaciones, etapas de creci-miento de plantas y humedad del suelo. Según Ruiz Rivera et al. (2016), conocer la extensión de un área permite conocer la magnitud de la cobertura espacial. Según lo mencionado anteriormente, la heterogeneidad de los valores, presentados en los mapas (Figura 3 y 5) relacionados con valores del NC, permiten categorizar los valores de NC y estimar la escorrentía superficial en puntos dentro de la unidad hidrográfica. Este valor, según Hong & Adler (2008) permite la evaluación de desastres por inundación. Hawkins et al. (2019) mencionan que los valores de NC, se pueden obtener de tablas estándar, los cuales están en función de los tipos de suelo y cobertura terrestre. Sin embargo, Ponce & Hawkins (1996) señalan que este método no tiene en cuenta la variabilidad espacial y temporal de la infiltración. Por otro lado, el producto de GCN250 propuesto por Jaafar et al. (2019), si considera la variabilidad espacial y temporal.
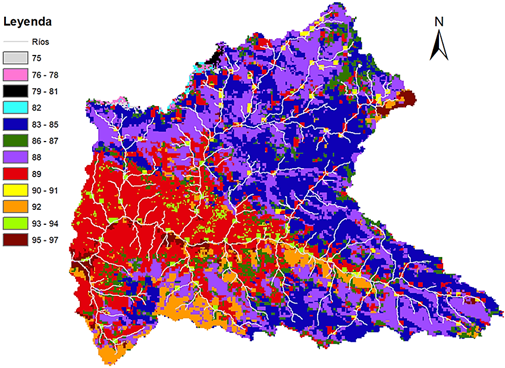
Figura 6. Distribución de valores de NC para condiciones de escorrentía antecedentes húmedas (ARCIII).
El producto GCN250 (Tabla 1), ofrece valores del NC presentados en cuadrículas, el cual utiliza a la cobertura terrestre y permite identificar al NC de cualquier zona específica (Alivio et al., 2024; Jaafar et al., 2019), a diferencia de los resultados de la Figura 2, donde no muestra la variabilidad espacial y temporal del NC de la zona de estudio.
Tabla 1
Comparacion de valores de NC para algunas zonas de la cuenca alta del Jequetepeque
|
Escenario |
Valor de GCN2250 para la cuenca Jequetepeque |
Número de curva global, por Jaafar et al. (2019) |
Ubicación de puntos en el área de estudio |
||||
|
P1 |
P2 |
P3 |
P4 |
P5 |
|||
|
ARC - I |
47-52 |
58-60 |
68-75 |
64 |
65-67 |
62 |
|
|
ARC - II |
67-71 |
76-77 |
76-77 |
67-71 |
76-77 |
78 |
|
|
ARC – III |
83-85 |
89 |
89 |
83-85 |
90-91 |
90 |
|
* Condición de escorrentía antecedente seca (ARC).
CONCLUSIONES
El producto global GCN250 es una herramienta de alta resolución espacial que permite identificar el Número de Curva para diferentes condiciones secas, promedio y húmedas para la cuenca alta del Jequetepeque. Haciendo uso del Sistema de Información Geográfica, se han obtenido tres condiciones de escorrentía para la cuenca alta de Jequetepeque expresados en mapas, estas son: (ARC I), (ARC II) y (ARC III), valores cercanos a cero indican alta infiltración y baja escorrentía superficial y por el contrario valores cercanos a 100 indican baja infiltración y una alta escorrentía. La condición ARC I, mostrados en el mapa de la cuenca alta del Jequetepeque, muestra una alta hetero-geneidad en los valores de NC. La condición ARC II, mostrados en el mapa de la cuenca alta del Jequetepeque, muestra heterogeneidad moderada en los valores de NC. La condición ARC III, mostrados en el mapa de la cuenca alta del Jequetepeque, muestra heterogeneidad baja en los valores de NC. El promedio de NC para la condición seca ARC I, es de 56,96, indica que la cuenca alta del Jequetepeque presenta una capacidad moderada de infiltración, con menor generación de escorrentía superficial. Esto es correcto al señalar suelos secos y menor saturación. El promedio de NC para la condición promedio ARC II, es de 74,5, indica que la capacidad de infiltración disminuye, pero aumenta la escorrentía. Esto puede reflejar suelos más húmedos, o mayor saturación en la cuenca, facilitando el escurrimiento superficial, y el promedio del NC para la condición humedad ARC III es de 86,53, indica baja capacidad de infiltración y alta escorrentía. Esta condición es característico en suelos saturados o condiciones muy húmedas, donde la generación de escorrentía es significativa. Se recomienda validar los valores de NC en las diferentes zonas de la cuenca en estudio, para el mejor manejo del recurso hídrico.
Es importante señalar la necesidad de desarrollar un Modelo Global de Numero de Curva a una menor resolución espacial, sobre todo en zonas altoandinas del territorio peruano.
REFERENCIAS BIBLIOGRÁFICAS
Ajmal, M., Waseem, M., Kim, D., & Kim, T. W. (2020). A Pragmatic Slope-Adjusted Curve Number Model to Reduce Uncertainty in Predicting Flood Runoff from Steep Watersheds. Water 2020, Vol. 12, Page 1469, 12(5), 1469. https://doi.org/10.3390/W12051469
Alivio, M. B., Radinja, M., Šraj, M., Gribovszki, Z., & Bezak, N. (2024). Comparative analysis of event runoff coefficients and curve numbers in contrasting urban environments based on observed rainfall-runoff data. Journal of Hydrology, 645, 132135. https://doi.org/10.1016/J.JHYDROL.2024.132135
Alvarez Villanueva, J. I., Huamán Vidaurre, J. F., Alvarez Villanueva, J. I., & Huamán Vidaurre, J. F. (2024). Usos de modelos hidrológicos para el cálculo del caudal ecológico del río Jequetepeque, aguas arriba de la presa “Gallito Ciego”, Perú. Manglar, 21(2), 217–226. https://doi.org/10.57188/MANGLAR.2024.023
Assaye, H., Nyssen, J., Poesen, J., Lemma, H., Meshesha, D. T., Wassie, A., Adgo, E., & Frankl, A. (2021). Curve number calibration for measuring impacts of land management in sub-humid Ethiopia. Journal of Hydrology: Regional Studies, 35, 100819. https://doi.org/10.1016/J.EJRH.2021.100819
Brandão, A. R. A., Schwamback, D., Ballarin, A. S., Ramirez-Avila, J. J., Vasconcelos Neto, J. G., & Oliveira, P. T. S. (2025). Toward a better understanding of curve number and initial abstraction ratio values from a large sample of watersheds perspective. Journal of Hydrology, 655, 132941. https://doi.org/10.1016/J.JHYDROL.2025.132941
Deshmukh, D. S., Chaube, U. C., Ekube Hailu, A., Aberra Gudeta, D., & Tegene Kassa, M. (2013). Estimation and comparision of curve numbers based on dynamic land use land cover change, observed rainfall-runoff data and land slope. Journal of Hydrology, 492, 89–101. https://doi.org/10.1016/J.JHYDROL.2013.04.001
Diaz Carvajal, A. D., & Mercado Fernández, T. (2017). Determinación del número de curva en la subcuenca de Betancí (Córdoba, Colombia) mediante teledetección y SIG. Ingeniería y Desarrollo, 35(2), 452–470.
Ekwule, O. R., & Agunwamba, J. C. (2024). Application of the NRCS-curve number method in humid tropical basins of southeastern Nigeria: a statistical analysis. Environmental Systems Research, 13(1), 1–16. https://doi.org/10.1186/S40068-024-00386-Z/FIGURES/6
Espinales Cedeño, F. R., Alulema del Salto, R. A., Caicedo Toro, M. D., Espinales Cedeño, F. R., Alulema del Salto, R. A., & Caicedo Toro, M. D. (2021). Determinación del Número de Curva (CN) de la cuenca del Río Portoviejo. Dilemas Contemporáneos: Educación, Política y Valores, 8(SPE2). https://doi.org/10.46377/DILEMAS.V8I.2600
Ferrer, M., Rodríguez, J., & Monreal, T. E. (1995). Generación automática del número de curva con sistemas de información geográfica. Ingeniería Del Agua, 2(4), 43–58. https://doi.org/10.4995/IA.1995.2686
Ferrer-Julià, M. (2002). Análisis de nuevas fuentes de datos para la estimación del parámetro número de curva: perfiles de suelos y teledetección. 1.
García-Guerrero, J. M., García, J. T., Alcaraz-Aparicio, M., Castillo, L. G., Altarejos-García, L., & Carrillo, J. M. (2021). Variabilidad del número de curva en función de las fuentes de datos en áreas cultivadas del sureste español. Ingeniería Del Agua, 25(4), 287–302. https://doi.org/10.4995/IA.2021.16013
Hawkins, R. H., Theurer, F. D., & Rezaeianzadeh, M. (2019). Understanding the Basis of the Curve Number Method for Watershed Models and TMDLs. Journal of Hydrologic Engineering, 24(7), 06019003. https://doi.org/10.1061/(ASCE)HE.1943-5584.0001755
Hawkins, R. H., Ward, R. H., Woodward, T. J., & Van Mullem, D. E. (2014). Curve Number Method: Time to Think Anew? Journal of Hydrologic Engineering, 19(6), 1059–1059. https://doi.org/10.1061/(ASCE)HE.1943-5584.0000954
Hong, Y., & Adler, R. F. (2008). Estimation of global SCS curve numbers using satellite remote sensing and geospatial data. International Journal of Remote Sensing, 29(2), 471–477. https://doi.org/10.1080/01431160701264292
Hope & Schulze. (1982). Improved estimates of stormflow volume using the SCS curve number method. Rainfall-runoff relationship/proceedings, International Symposium on Rainfall-Runoff Modeling.
Huang, M., Gallichand, J., Wang, Z., & Goulet, M. (2006). A modification to the Soil Conservation Service curve number method for steep slopes in the Loess Plateau of China. Hydrological Processes, 20(3), 579–589. https://doi.org/10.1002/HYP.5925
Jaafar, H. H., Ahmad, F. A., & El Beyrouthy, N. (2019). GCN250, new global gridded curve numbers for hydrologic modeling and design. Scientific Data, 6(1), 1–9. https://doi.org/10.1038/s41597-019-0155-x
Kowalik, T., & Walega, A. (2015). Estimation of CN Parameter for Small Agricultural Watersheds Using Asymptotic Functions. Water, 7(3), 939–955. https://doi.org/10.3390/W7030939
Lee, K. K. F., Ling, L., & Yusop, Z. (2023). The Revised Curve Number Rainfall–Runoff Methodology for an Improved Runoff Prediction. Water 15(3), 491. https://doi.org/10.3390/W15030491
Lian, H., Yen, H., Huang, J. C., Feng, Q., Qin, L., Bashir, M. A., Wu, S., Zhu, A. X., Luo, J., Di, H., Lei, Q., & Liu, H. (2020). CN-China: Revised runoff curve number by using rainfall-runoff events data in China. Water Research, 177, 115767. https://doi.org/10.1016/J.WATRES.2020.115767
Manuel García-Guerrero, J., Tomás García, J., Alcaraz-Aparicio, M., Gerardo Castillo, L., Altarejos-García, L., María Carrillo, J., como, C., Manuel, J., Tomás, J., & Gerardo, L. (2021). Variabilidad del número de curva en función de las fuentes de datos en áreas cultivadas del sureste español. Ingeniería Del Agua, 25(4), 287–302. https://doi.org/10.4995/IA.2021.16013
Mejia, V., Orellana, D., & Cabrera, P. (2021). Cambio de uso de suelo en la Amazonía norte del Ecuador: un análisis a través de imágenes satelitales nocturnas VIIRS e imágenes LANDSAT. Universidad-Verdad, 78, 10–29. https://doi.org/10.33324/UV.V1I1.355
Mishra, S. K., Singh, V. P., & Singh, P. K. (2018). Revisiting the Soil Conservation Service Curve Number Method. 667–693. https://doi.org/10.1007/978-981-10-5801-1_46
Pacheco Moya, R. M., Quiala Ortiz, E., & Martínez Hernández, I. (2018). Determinación del parámetro número de curva en la cuenca Las Coloradas en un entorno SIG. Ingeniería Hidráulica y Ambiental, 39(2), 60–71.
Pérez-Corredor, L., Hume, S. E., Alivio, M. B., & Bezak, N. (2024). Exploring the Impact of Nature-Based Solutions for Hydrological Extremes Mitigation in Small Mixed Urban-Forest Catchment. Applied Sciences (Switzerland), 14(24), 11813. https://doi.org/10.3390/APP142411813/S1
Ponce, V. M., & Hawkins, R. H. (1996). Runoff Curve Number: Has It Reached Maturity? Journal of Hydrologic Engineering, 1(1), 11–19. https://doi.org/10.1061/(ASCE)1084-0699(1996)1:1(11)
Ruiz Rivera, N., Galicia, L., Ruiz Rivera, N., & Galicia, L. (2016). La escala geográfica como concepto integrador en la comprensión de problemas socio-ambientales. Investigaciones Geográficas, 89(89), 137–153. https://doi.org/10.14350/RIG.47515
Serie de capacitación en hidrología para ingeniería del NEDC. (1997). Módulo 205: Ecuación de escorrentía SCS. NEDC.
Sobral, G. S., Jerónimo Leyton, N., Ramirez Avila, J. J., & Rengifo Montufar, H. (2025). Método de Curva Número: Herramienta para el Manejo de Recursos Hídricos. Siembra, 12(4), e8295–e8295.
Tedela, N. H., McCutcheon, S. C., Rasmussen, T. C., Hawkins, R. H., Swank, W. T., Campbell, J. L., Adams, M. B., Jackson, C. R., & Tollner, E. W. (2011). Runoff Curve Numbers for 10 Small Forested Watersheds in the Mountains of the Eastern United States. Journal of Hydrologic Engineering, 17(11), 1188–1198. https://doi.org/10.1061/(ASCE)HE.1943-5584.0000436
Theochari, A. P., & Baltas, E. (2024). The Nature-Based Solutions and climate change scenarios toward flood risk management in the greater Athens area—Greece. Natural Hazards, 120(5), 4729–4747. https://doi.org/10.1007/S11069-024-06409-3/FIGURES/8
Zhang, Y., Xia, J., Yu, J., Randall, M., Zhang, Y., Zhao, T., Pan, X., Zhai, X., & Shao, Q. (2018). Simulation and assessment of urbanization impacts on runoff metrics: insights from landuse changes. Journal of Hydrology, 560, 247–258. https://doi.org/10.1016/J.JHYDROL.2018.03.031